摘要:1.曲线方程 方程的方法及其具体步骤如下: 步 骤 含 义 说 明 1.“建 :建立坐标系,“设 :设动点坐标. 建立适当的直角坐标系.用(x,y)表示曲线上任意一点M的坐标. (1) 所研究的问题已给出坐标系.即可直接设点. (2) 没有给出坐标系.首先要选取适当的坐标系. 2.现(限):由限制条件.列出几何等式. 写出适合条件P的点M的集合P={M|P(M)} 这是求曲线方程的重要一步.应仔细分析题意.使写出的条件简明正确. 3.“代 :代换 用坐标法表示条件P=0 常常用到一些公式. 4.“化 :化简 化方程f(x,y)=0为最简形式. 要注意同解变形. 5.证明 证明化简以后的方程的解为坐标的点都是曲线上的点. 化简的过程若是方程的同解变形.可以不要证明.变形过程中产生不增根或失根.应在所得方程中删去或补上(即要注意方程变量的取值范围). 这五个步骤可浓缩为五字“口诀 :建设现(限)代化 (2)求曲线方程的常见方法: 直接法:也叫“五步法 .即按照求曲线方程的五个步骤来求解.这是求曲线方程的基本方法. 转移代入法:这个方法又叫相关点法或坐标代换法.即利用动点是定曲线上的动点.另一动点依赖于它.那么可寻求它们坐标之间的关系.然后代入定曲线的方程进行求解. 几何法:就是根据图形的几何性质而得到轨迹方程的方法. 参数法:根据题中给定的轨迹条件.用一个参数来分别动点的坐标.间接地把坐标x,y联系起来.得到用参数表示的方程.如果消去参数.就可以得到轨迹的普通方程.
网址:http://m.1010jiajiao.com/timu_id_4393038[举报]
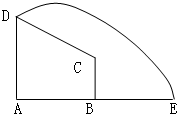 如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,BC=| 3 |
(1)建立恰当的直角坐标系,求曲线L的方程;
(2)根据曲线L的方程写出曲线段DE(含两端点)的方程;
(3)若点M为曲线段DE(含两端点)上的任一点,试求|MC|+|MA|的最小值,并求出取得最小值时点M的坐标. 查看习题详情和答案>>
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点P(m,n)在曲线段C上,直线l:mx+ny=1,求直线l被圆x2+y2=1截得的弦长的取值范围.
(本小题满分14分)
如图,直线 和
和 相交于点
相交于点 且
且 ,点
,点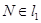 .以
.以 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到 的距离与到点
的距离与到点 的距离相等.若
的距离相等.若 为锐角三角形,
为锐角三角形, ,
, ,且
,且 .
.
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点 在曲线段C上,直线
在曲线段C上,直线 ,求直线
,求直线 被圆
被圆 截得的弦长的取值范围.
截得的弦长的取值范围.

查看习题详情和答案>>
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6. ,点E在线段AB的延长线上.若曲线段DE(含两端点)为某曲线L上的一部分,且曲线L上任一点到A、B两点的距离之和都相等.
,点E在线段AB的延长线上.若曲线段DE(含两端点)为某曲线L上的一部分,且曲线L上任一点到A、B两点的距离之和都相等.