摘要：(1)解:由f(x1+x2)＝f(x1)·f(x2).x1.x2∈［0.］知 f(x)=f()·f()≥0.x∈［0.1］.∵f(1)=f(+)=f()·f()= [f()]2.f(1)＝2.∴f()＝2． ∵f()=f(+)=f()·f()=[f()]2.f()=2. ∴f()=2． (2)证明:依题设y=f(x)关于直线x=1对称. ∴f(x)=(1+1-x).f(x)=f(2-x) 又∵f(-x)=f(x).∴f(-x)=f(2-x).∴f(x)=f(2+x). ∴f(x)是R上的周期函数.且2是它的一个周期．
网址：http://m.1010jiajiao.com/timu_id_4392398[举报]
设x1和x2是方程x2+(t-3)x+(t2-24)＝0的两个实根,定义函数f(t)=logm(x12+x22)(m＞1)，求函数y=f(t)的单调区间，并说明理由.
思路点拨：要想求函数y=f(t)的单调区间，首先要求函数y=f(t)的解析式及定义域.如果在整个定义域内函数不是单调的，那就要把定义域分成几个函数具有单调性的区间段，从而确定单调区间.
查看习题详情和答案>>解答题：解答应写出文字说明，证明过程或演算步骤．
设P(x1，y1)，Q(x2，y2)是抛物线C：y2＝2px(p＞0)上相异两点，且
，直线PQ与x轴相交于E．
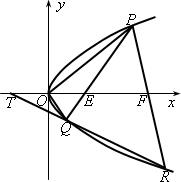
(Ⅰ)若P，Q到x轴的距离的积为4，求p的值；
(Ⅱ)若p为已知常数，在x轴上，是否存在异于E的一点F，使得直线PF与抛物线的另一交点为R，而直线RQ与x轴相交于T，且有
，若存在，求出F点的坐标(用p表示)，若不存在，说明理由．
已知函数
在x＝1处取得极值2．
(1)求f(x)的解析式；
(2)设A是曲线y＝f(x)上除原点O外的任意一点，过OA的中点且垂直于x轴的直线交曲线于点B，试问：是否存在这样的点A，使得曲线在点B处的切线与OA平行？若存在，求出点A的坐标；若不存在，说明理由；
(3)设函数g(x)＝x2－2ax＋a，若对于任意x1∈R，总存在x2∈[－1，1]，使得g(x2)≤f(x1)，求实数a的取值范围．