Question

解答题：解答应写出文字说明，证明过程或演算步骤．

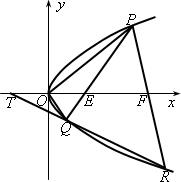
设P(x₁，y₁)，Q(x₂，y₂)是抛物线C：y²＝2px(p＞0)上相异两点，且，直线PQ与x轴相交于E．

(Ⅰ)若P，Q到x轴的距离的积为4，求p的值；

(Ⅱ)若p为已知常数，在x轴上，是否存在异于E的一点F，使得直线PF与抛物线的另一交点为R，而直线RQ与x轴相交于T，且有，若存在，求出F点的坐标(用p表示)，若不存在，说明理由．

Answer 1

答案：
解析：

解：(Ⅰ)∵＝0，则x1x2＋y1y2＝0，　　1分 　　又P、Q在抛物线上， 　　∴y12＝2px1，y22＝2px2， 　　∴＋y1y2＝0，y1y2＝－4p2， 　　∴|y1y2|＝4p2，　　3分 　　又|y1y2|＝4，∴4p2＝4，p＝1．　　4分 　　(Ⅱ)设E(a，0)，直线PQ方程为x＝my＋a， 　　联立方程组，　　5分 　　消去x得y2－2pmy－2pa＝0，　　6分 　　∴y1y2＝－2pa，　　①　　7分 　　设F(b，0)，R(x3，y3)，同理可知： 　　y1y3＝－2pb，　　②　　8分 　　由①、②可得，　　③　　9分 　　若，设T(c，0)，则有 　　(x3－c，y3－0)＝3(x2－c，y2－0)， 　　∴y3＝3y2　　即　＝3，　　④　　10分 　　将④代入③，得　b＝3a．　　11分 　　又由(Ⅰ)知，＝0， 　　∴y1y2＝－4p2，代入①， 　　得－2pa＝－4p2　　∴a＝2p，　　13分 　　∴b＝6p， 　　故，在x轴上，存在异于E的一点F(6p，0)，使得．　　14分 　　注：若设直线PQ的方程为y＝kx＋b，不影响解答结果．