摘要:(1)证明:根据题设.对任意x∈R.都有f(x)≤1.又f(x)=-b(x-)2+.∴f()=≤1.∵a>0.b>0.∴a≤2. (2)证明:必要性:对任意x∈[0.1].|f(x)|≤1f(x)≥-1.据此可推出 f(1)≥-1.即a-b≥-1.∴a≥b-1. 对任意x∈[0.1].|f(x)|≤1f(x)≤1.因为b>1.可得0<<1.可推出f()≤1.即a·-1≤1.∴a≤2.∴b-1≤a≤2. 充分性:因为b>1.a≥b-1.对任意x∈[0.1].可以推出ax-bx2≥b(x-x2)-x≥-x≥-1.即ax-bx2≥-1.因为b>1.a≤2.对任意x∈[0.1].可以推出: ax-bx2≤2x-bx2-b(x-)2+1≤1.即ax-bx2≤1.∴-1≤f(x)≤1. 综上.当b>1时.对任意x∈[0.1].|f(x)|≤1的充要条件是b-1≤a≤2. (3)解:因为a>0.0<b≤1时.对任意x∈[0.1]有f(x)=ax-bx2≥-b≥-1.即f(x)≥-1, f(x)≤1f(1)≤1a-b≤1.即a≤b+1.又a≤b+1f(x)≤(b+1)x-bx2≤1.即f(x)≤1. 所以.当a>0.0<b≤1时.对任意x∈[0.1].|f(x)|≤1的充要条件是a≤b+1. 评述:本题主要考查二次函数.不等式.充要条件的综合运用.考查分类讨论思想和逻辑推理能力以及思维能力.
网址:http://m.1010jiajiao.com/timu_id_4392397[举报]
(本题满分14分)设直线![]() . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有![]() . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数![]() .求证:
.求证:![]() 为曲线
为曲线![]() 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
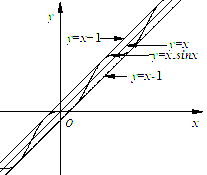

根据上图,试推测曲线![]() 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.

 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.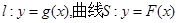 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有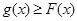 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.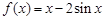 .求证:
.求证: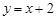 为曲线
为曲线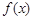 的“上夹线”.
的“上夹线”.
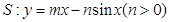 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.