摘要:解:原不等式变形为:log(x2-x-2)>log(2x-2).所以.原不等式 故原不等式的解集为{x|2<x<3}. 评述:本题通过对数恒等变形.转化为函数单调性问题.考查了考生的演绎推理和逻辑思维及计算能力. ※90.解:(1)当每辆车的月租金定为3600元时.未租出的车辆数为: =12.所以这时租出了88辆车. (2)设每辆车的月租金定为x元.则租赁公司的月收益为:f(x)=(100-)(x-150)-×50.整理得:f(x)=-+162x-21000=-(x-4050)2+307050.所以.当x=4050时.f(x)最大.其最大值为f=307050.即当每辆车的月租金定为4050元时.租赁公司的月收益最大.最大收益为307050元. 评述:本题贴近生活.要求考生读懂题目.迅速准确建立数学模型.把实际问题转化为数学问题并加以解决.
网址:http://m.1010jiajiao.com/timu_id_4392386[举报]
解关于 的不等式:
的不等式:

【解析】解:当 时,原不等式可变为
时,原不等式可变为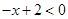 ,即
,即 (2分)
(2分)
当 时,原不等式可变为
时,原不等式可变为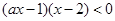
 (5分) 若
(5分) 若 时,
时, 的解为
的解为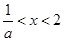 (7分)
(7分)
若 时,
时, 的解为
的解为 (9分) 若
(9分) 若 时,
时, 无解(10分) 若
无解(10分) 若 时,
时, 的解为
的解为 (12分综上所述
(12分综上所述
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为:
时,原不等式的解为: 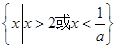
查看习题详情和答案>>
三个同学对问题“关于x的不等式x2+25+|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于x的函数,作出函数图象”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是 .
查看习题详情和答案>>
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于x的函数,作出函数图象”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是
(2011•上海)为求方程x5-1=0的虚根,可以把原方程变形为(x-1)(x2+ax+1)(x2+bx+1)=0,由此可得原方程的一个虚根为
.
查看习题详情和答案>>
-1-
| ||||||
| 4 |
-1-
| ||||||
| 4 |
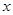 的不等式
的不等式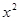 +25+|
+25+|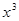 -5
-5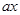 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数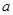 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.