摘要：(上海)设是定义在正整数集上的函数.且满足:“当成立时.总可推出成立 ．那么.下列命题总成立的是 若成立.则当时.均有成立 若成立.则当时.均有成立 若成立.则当时.均有成立 若成立.则当时.均有成立 (湖南)已知函数,数列{}满足: ..求证: ;. (江西)已知数列满足:.且(≥.) 求数列的通项公式,求证:对于一切正整数.不等式 (湖北)已知为正整数. 用数学归纳法证明:当时.≥, 对于≥.已知.求证., 求出满足等式的所有正整数.
网址：http://m.1010jiajiao.com/timu_id_4389775[举报]
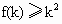成立时，总可推出，
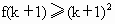成立”．那么，下列命题总成立的是
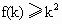成立
成立
是定义在正整数集上的函数，且
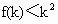成立时，总可推出
成立”． 那么，下列命题总成立的是（ ）
成立，则
成立
成立，则
成立
成立，则当
时，均有
成立
成立，则当
时，均有