摘要:在几何问题中.有些几何量与参数无关.这就构成了定值问题.解决这类问题一种思路是进行一般计算推理求出其结果,另一种是通过考查极端位置.探索出“定值 是多少.然后再进行一般性证明或计算.即将该问题涉及的几何式转化为代数式或三角形式.证明该式是恒定的.如果试题以客观题形式出现.特殊方法往往比较奏效. 对满足一定条件曲线上两点连结所得直线过定点或满足一定条件的曲线过定点问题.设该直线上两点的坐标.利用坐标在直线上.建立点的坐标满足的方程(组).求出相应的直线.然后再利用直线过定点的知识加以解决. 解析几何的最值和范围问题.一般先根据条件列出所求目标的函数关系式.然后根据函数关系式的特征选用参数法.配方法.判别式法.不等式法.单调性法.导数法以及三角函数最值法等求出它的最大值和最小值. (二)典例分析: 问题1. (广东)在平面直角坐标系中. 抛物线上异于坐标原点的两不同动点.满足. (Ⅰ)求得重心的轨迹方程, (Ⅱ)的面积是否存在最小值?若存在.请求出最小值, 若不存在.请说明理由. 问题2.已知椭圆上的两个动点及定点 .为椭圆的左焦点.且..成等差数列.求证:线段的垂直平分线经过一个定点, 设点关于原点的对称点是.求的最小值及相应的点坐标. 问题3.(全国Ⅱ)已知抛物线的焦点为..是抛物线上的两动点.且().过.两点分别作抛物线的切线.设其交点为. (Ⅰ)证明为定值, (Ⅱ)设的面积为.写出的表达式.并求的最小值. 问题4.直线:和双曲线的左支交于.两点.直线过点和线段的中点.求在轴上的截距的取值范围.
网址:http://m.1010jiajiao.com/timu_id_4389691[举报]
为配合新课程的实施,乌鲁木齐市第一中学联合兄弟学校举行了“应用与创新”知识竞赛,共有1500名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
|
组别 |
分 组 |
频 数 |
频率 |
|
1 |
49.5~59.5 |
60 |
0.12 |
|
2 |
59.5~69.5 |
120 |
0.24 |
|
3 |
69.5~79.5 |
180 |
0.36 |
|
4 |
79.5~89.5 |
130 |
|
|
5 |
89.5~99.5 |
|
0.02 |
|
合 计 |
|
1.00 |
解答下列问题:
(1)在这个问题中,总体是 ,样本是 ,
样本容量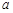 =
;
=
;
(2)第四小组的频率 =
;
=
;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计此次竞赛获一等奖的人数.
查看习题详情和答案>>
某厂生产甲产品每千克需用原料A和原料B分别为a1、b1千克,生产乙产品每千克需用原料A和原料B分别为a2、b2千克.甲、乙产品每千克可获利润分别为d1、d2元.月初一次性购进本月用原料A、B各c1、c2千克.要计划本月生产甲、乙两种产品各多少千克才能使月利润总额达到最大.在这个问题中,设全月生产甲、乙两种产品分别为x千克、y千克,月利润总额为z元,那么,用于求使总利润z=d1x+d2y最大的数学模型中,约束条件为( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
