题目内容

给出以下四个命题：

①动点到两定点的距离之和为4,则点的轨迹为椭圆；

②为抛物线上一点，为焦点，定点，则的最小值3；

③函数在上单调递增；

④定义在R上的可导函数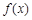满足，，则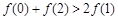

一定成立.其中，所有真命题的序号是           .

 

【答案】

②③④

【解析】解：因为

①动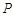点到两定点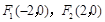的距离之和为4，则点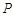的轨迹为线段，错误。

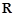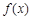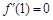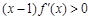②设定义在上的可导函数满足，，则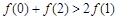一定成立；成立

③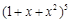展开式中，含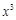项的系数为30；成立

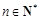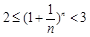④若，则.成立

 

练习册系列答案
相关题目
8、已知数列A：a1，a2，…，an（0≤a1＜a2＜…＜an，n≥3）具有性质P：对任意i，j（1≤i≤j≤n），aj+ai与aj-ai两数中至少有一个是该数列中的一项、现给出以下四个命题：①数列0，1，3具有性质P；②数列0，2，4，6具有性质P；③若数列A具有性质P，则a1=0；④若数列a1，a2，a3（0≤a1＜a2＜a3）具有性质P，则a1+a3=2a2，其中真命题有（　　）
定义平面向量之间的一种运算“*”如下：对任意的
a
=(m，n)，
b
=(p，q)，令
a
*
b
=mq-np．给出以下四个命题：（1）若
a
与
b
共线，则
a
*
b
=0；（2）
a
*
b
=
b
*
a
；（3）对任意的λ∈R，有(λ
a
)*
b
=λ(
a
*
b
)（4）(
a
*
b
)2+(
a
•
b
)2=|
a
|2•|
b
|2．（注：这里
a
•
b
指
a
与
b
的数量积）则其中所有真命题的序号是（　　）
A、（1）（2）（3）
B、（2）（3）（4）
C、（1）（3）（4）
D、（1）（2）（4）
如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′交于M、N，设BM=x，x∈[0，1]，给出以下四个命题：
①平面MENF⊥平面BDD′B′；
②当且仅当x=
12
时，四边形MENF的面积最小；
③四边形MENF周长l=f（x），x∈0，1]是单调函数；
④四棱锥C′-MENF的体积v=h（x）为常函数；
以上命题中真命题的序号为
①②④
①②④
．
若整数m满足不等式x-
1
2
≤m＜x+
1
2
，x∈R，则称m为x的“亲密整数”，记作{x}，即{x}=m，已知函数f（x）x-{x}．给出以下四个命题：
①函数y=f（x），x∈R是周期函数且其最小正周期为1；
②函数y=f（x），x∈R的图象关于点（k，0），k∈Z中心对称；
③函数y=f（x），x∈R在[-
1
2
，
1
2
]上单调递增；
④方程f(x)=
1
2
sin(π•x)在[-2，2]上共有7个不相等的实数根．
其中正确命题的序号是
①④
①④
．（写出所有正确命题的序号）．
给出以下四个命题：
①函数f(x)=sinx+2xf′(
π
3
)，f′（x）为f（x）的导函数，令a=log32，b=
1
2
，则f（a）＜f（b）
②若f(x+2)+
1
f(x)
=0，则函数y=f（x）是以4为周期的周期函数；
③在数列{an}中，a1=1，Sn是其前n项和，且满足Sn+1=
1
2
Sn+2，则数列{an}是等比数列；
④函数y=3x+3-x（x＜0）的最小值为2．
则正确命题的序号是
①②
①②
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网