摘要：问题1．(武汉调研)如果命题“坐标满足方程的点都在曲线上 是不正确的.那么下列命题正确的是 坐标满足方程的点都不在曲线上, 曲线上的点不都满足方程,坐标满足方程的点有些在曲线上.有些不在曲线上,至少有一个点不在曲线上.其坐标满足方程. 如果曲线上的点满足方程.则以下说法正确的是: 曲线的方程是,方程的曲线是, 坐标满足方程的点在曲线上, 坐标不满足方程的点不在曲线上, 判断下列结论的正误.并说明理由: ① 过点且垂直于轴的直线的方程为, ②到轴距离为的点的直线的方程为, ③到两坐标轴的距离乘积等于的点的轨迹方程为, ④的顶点...为的中点.则中线的方程为. 作出方程所表示的曲线. 问题2．设动直线垂直于轴.且与椭圆交于两点.是上满足的点.求点的轨迹方程. 问题3．已知中...所对的边分别为.且 成等差数列..求顶点的轨迹方程. 问题4．若动点在上移动.求与连线中点的轨迹方程 问题5．已知抛物线.为顶点. 为抛物线上的两动点.且.如果 于.求点的轨迹方程.
网址：http://m.1010jiajiao.com/timu_id_4389653[举报]
问题1：已知函数f(x)=
，则f(
)+f(
)+…+f(
)+f(1)+f(2)+…+f（9）+f（10）=
．
我们若把每一个函数值计算出，再求和，对函数值个数较少时是常用方法，但函数值个数较多时，运算就较繁锁．观察和式，我们发现f(
)+f(2)、…、f(
)+f(9)、f(
)+f(10)可一般表示为f(
)+f(x)=
+
=
+
=
=1为定值，有此规律从而很方便求和，请求出上述结果，并用此方法求解下面问题：
问题2：已知函数f(x)=
，求f（-2007）+f（-2006）+…+f（-1）+f（0）+f（1）+…+f（2007）+f（2008）的值．
查看习题详情和答案>>
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
我们若把每一个函数值计算出，再求和，对函数值个数较少时是常用方法，但函数值个数较多时，运算就较繁锁．观察和式，我们发现f(
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
问题2：已知函数f(x)=
| 1 | ||
2x+
|
17、如图，是求[1，1000]内所有奇数的和的一个程序框图，阅读理解
（1）教材27页有如下内容：
分别观察三个图象，你看出哪些变化规律
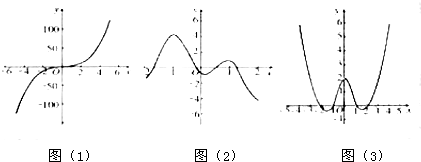
（2）教材是这样定义偶函数的（如图文字）
问题1：辅导班的小王认为 f（x）=x2，x∈[-5，5）是偶函数，理由如下：对于函数定义域内的任意一个x，f（-x）=（-x）2=x2=f（x），所以该函数式偶函数，你认为对吗？为什么？
问题2：奇函数的定义是？
查看习题详情和答案>>
（1）教材27页有如下内容：
分别观察三个图象，你看出哪些变化规律
（2）教材是这样定义偶函数的（如图文字）
问题1：辅导班的小王认为 f（x）=x2，x∈[-5，5）是偶函数，理由如下：对于函数定义域内的任意一个x，f（-x）=（-x）2=x2=f（x），所以该函数式偶函数，你认为对吗？为什么？
问题2：奇函数的定义是？
国家统计局发布最新数据显示，2011年11月份全国副省级城市中CPI（消费指数）值位于前15位的城市具体情况如下表：
（1）求这15个城市CPI值的平均值及众数
（2）完成下表：
（3）从[103.0，104.0]区间内随机选取2城市，求恰有1个城市CPI的值在[103.5，104.0）中的概率．
查看习题详情和答案>>
| 城市 | CPI | 序号 | 城市 | CPI | 序号 |
| 济南 | 105.2 | 1 | 青岛 | 104.7 | 2 |
| 广州 | 104.6 | 3 | 西安 | 104.4 | 4 |
| 哈尔滨 | 104.3 | 5 | 厦门 | 104.2 | 6 |
| 杭州 | 104.1 | 7 | 武汉 | 104.1 | 8 |
| 深圳 | 104.1 | 9 | 南京 | 103.9 | 10 |
| 长春 | 103.9 | 11 | 沈阳 | 103.6 | 12 |
| 大连 | 103.3 | 13 | 成都 | 103.0 | 14 |
| 宁波 | 102.6 | 15 |
（2）完成下表：
| CPI | [102.5，103.0） | [103.0，103.5） | [103.5，104.0） | [104.0，104.5） | [104.5，105.0） | [105.0，105.5） |
| 频数 |