题目内容
问题1:求三维空间至多被n个平面分割的区域数F(n).
问题2:求一个平面至多被n条直线分割的区域数G(n).
问题3:求一直线至多被n个点分成的段数S(n).
问题2:求一个平面至多被n条直线分割的区域数G(n).
问题3:求一直线至多被n个点分成的段数S(n).
分析:把n=1,2 3,4的情况整理成表,于是归纳出一般的结论:G(n)=G(n-1)+S(n-1),F(n)=F(n-1)+
G(n-1),再由 G(n)=
=
+
+
,可得F(n)=F(1)+
+
+
=
+
+
+
(n≥),还可进一步归纳出更一般的结论:m维空间最多能被n个m-1维平面分割的区域数为
=
+
+…
.
G(n-1),再由 G(n)=
| n2+n+2 |
| 2 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| n-1 |
 |
| i=1 |
| C | i 0 |
| n-1 |
 |
| i=1 |
| C | i 1 |
| n-1 |
 |
| i-2 |
| C | i 2 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| E | (n) m |
| C | 0 n |
| C | 1 n |
| C | m n |
解答:解:先考虑特殊情况:F(1)=2,F(2)=4,F(3)=8,但凭借几何直观难以想象n=4的情况,
于是转向考虑平面上类似问题.
先考虑特殊情况:G(1)=2,G(2)=4,G(3)=7,G(4)=11,但是随着直线数目的增多,情况越来越复杂,
不能立即得出G(n)的一般表达式.于是,通过类比进一步考虑更简单的问题,一直线至多被n个点分成的段数
S(n).显然,这个问题易解决.S(1)=2,S(2)=3,…,S(n)=n+1.
将以上讨论的结果整理成下表:
观察上表,发现G(n)和S(n)列中两列数之和,等于G(n)的下一列中的数字;F(n)和G(n)列中的并列两数
之和等于F(n)的下一行中的数字,于是归纳出一般的结论:G(n)=G(n-1)+S(n-1),
F(n)=F(n-1)+G(n-1).
这个结论是否正确?如果正确,又应怎样进行证明呢?
再从特殊情况进行分析:三条直线分成七个部分,第四条直线l与前三条直线均相交,三个交点为A1,A2,A3.
直线l所穿过的区域均被l分为两部分,于是增加的区域数就等于直线l穿过的区域数S(3),
而直线l穿过的区域数等于l被点A1,A2,A3分成的段数S(3),于是,G(4)=G(3)+S(3).
对n=4的分析,可以一字不差地适用于一般情况 G(n)=G(n-1)+S(n-1)的证明.
这样,G(n)=G(n-1)+n,故 G(n)=
=
+
+
.
关于平面G(n)的表达式的推导也可以类比到三维空间,于是,F(n)=F(n-1)+G(n-1),F(n)=F(1)+
+
+
=2+(n-1)+
+
=
+
+
+
(n≥3),
这样,刚开始提出的三个问题均得到圆满的解决.
当然,如果把S(n)=n+1记为S(n)=
+
,那么,由S(n),G(n)、F(n)的表达式可以
归纳出更一般的结论:
m维空间最多能被n个m-1维平面分割的区域数,
=
+
+…
.
于是转向考虑平面上类似问题.
先考虑特殊情况:G(1)=2,G(2)=4,G(3)=7,G(4)=11,但是随着直线数目的增多,情况越来越复杂,
不能立即得出G(n)的一般表达式.于是,通过类比进一步考虑更简单的问题,一直线至多被n个点分成的段数
S(n).显然,这个问题易解决.S(1)=2,S(2)=3,…,S(n)=n+1.
将以上讨论的结果整理成下表:
| 分割元素的数目n | 被割出的数目 | ||
| 空间被平面F(n) | 平面被直线G(n) | 直线被点S(n) | |
| 1 | 2 | 2 | 2 |
| 2 | 4 | 4 | 3 |
| 3 | 8 | 7 | 4 |
| 4 | ? | 11 | 5 |
| … | ? | ? | … |
| n | ? | ? | n+1 |
之和等于F(n)的下一行中的数字,于是归纳出一般的结论:G(n)=G(n-1)+S(n-1),
F(n)=F(n-1)+G(n-1).
这个结论是否正确?如果正确,又应怎样进行证明呢?
再从特殊情况进行分析:三条直线分成七个部分,第四条直线l与前三条直线均相交,三个交点为A1,A2,A3.
直线l所穿过的区域均被l分为两部分,于是增加的区域数就等于直线l穿过的区域数S(3),
而直线l穿过的区域数等于l被点A1,A2,A3分成的段数S(3),于是,G(4)=G(3)+S(3).
对n=4的分析,可以一字不差地适用于一般情况 G(n)=G(n-1)+S(n-1)的证明.
这样,G(n)=G(n-1)+n,故 G(n)=
| n2+n+2 |
| 2 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
关于平面G(n)的表达式的推导也可以类比到三维空间,于是,F(n)=F(n-1)+G(n-1),F(n)=F(1)+
| n-1 |
 |
| i=1 |
| C | 0 i |
| n-1 |
 |
| i=1 |
| C | 1 i |
| n-1 |
 |
| i-2 |
| C | 2 i |
| C | 2 n |
| C | 3 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
这样,刚开始提出的三个问题均得到圆满的解决.
当然,如果把S(n)=n+1记为S(n)=
| C | 0 n |
| C | 1 n |
归纳出更一般的结论:
m维空间最多能被n个m-1维平面分割的区域数,
| E | (n) m |
| C | 0 n |
| C | 1 n |
| C | m n |
点评:本题主要考查的知识点是归纳推理,由特殊的例子得到一般性的结论,属于中档题.本题较抽象,不易下手,易因为无法下手而导致解题失败

练习册系列答案
相关题目

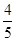 ;若使用其中未校正的枪,每射击一次击中目标的概率为
;若使用其中未校正的枪,每射击一次击中目标的概率为 ,假定每次射击是否击中目标相互之间没有影响。
,假定每次射击是否击中目标相互之间没有影响。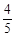 、
、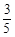 、
、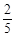 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。