题目内容
过抛物线C: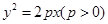 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求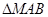 面积的最大值.
面积的最大值.
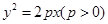 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求
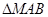 面积的最大值.
面积的最大值.(1)y2=8x,(2,4);(2) .
.
 .
.试题分析:本题主要考查抛物线的标准方程及其几何性质、韦达定理、点到直线的距离、三角形面积公式、利用导数求函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,由题意结合抛物线图象得到M点坐标,代入抛物线方程中,解出P的值,从而得到抛物线的标准方程及M点坐标;第二问,设出A,B点坐标,利用M点,分别得到直线MA和直线MB的斜率,因为两直线倾斜角互补,所以两直线的斜率相加为0,整理得到y1+y2=-8,代入到
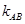 中得到直线AB的斜率,设出直线AB的方程,利用M点在直线AB上方得到b的范围,令直线与抛物线方程联立,图形有2个交点,所以方程的
中得到直线AB的斜率,设出直线AB的方程,利用M点在直线AB上方得到b的范围,令直线与抛物线方程联立,图形有2个交点,所以方程的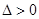 进一步缩小b的范围,
进一步缩小b的范围,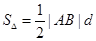 ,而
,而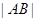 用两点间距离公式转化,d是M到直线AB的距离,再利用导数求面积的最大值.
用两点间距离公式转化,d是M到直线AB的距离,再利用导数求面积的最大值.(1)抛物线C的准线x=-
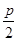 ,依题意M(4-
,依题意M(4-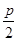 ,4),
,4),则42=2p(4-
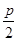 ),解得p=4.
),解得p=4.故抛物线C的方程为y2=8x,点M的坐标为(2,4), 3分
(2)设
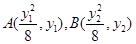 .
.直线MA的斜率
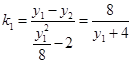 ,同理直线MB的斜率
,同理直线MB的斜率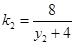 .
.由题设有
 ,整理得y1+y2=-8.
,整理得y1+y2=-8.直线AB的斜率
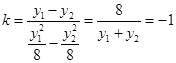 . 6分
. 6分设直线AB的方程为y=-x+b.
由点M在直线AB的上方得4>-2+b,则b<6.
由
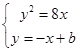 得y2+8y-8b=0.
得y2+8y-8b=0.由Δ=64+32b>0,得b>-2.于是-2<b<6. 9分
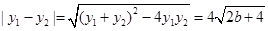 ,
,于是
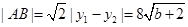 .
.点M到直线AB的距离
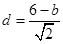 ,则△MAB的面积
,则△MAB的面积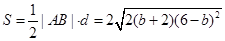 .
.设f(b)=(b+2)(6-b)2,则f¢(b)=(6-b)(2-3b).
当
 时,f¢(x)>0;当
时,f¢(x)>0;当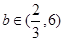 时,f¢(x)<0.
时,f¢(x)<0.当
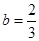 时,f(b)最大,从而S取得最大值
时,f(b)最大,从而S取得最大值 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 分别是椭圆
分别是椭圆 的左、右焦点,过点
的左、右焦点,过点 的直线交椭圆
的直线交椭圆 于
于 两点,若
两点,若 轴,则椭圆
轴,则椭圆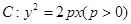 过点
过点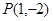 .
.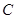 的方程,并求其准线方程;
的方程,并求其准线方程;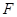 且斜率为
且斜率为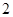 的直线
的直线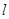 与抛物线交于
与抛物线交于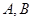 两点,求
两点,求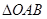 的面积.
的面积.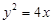 上一点
上一点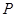 到直线
到直线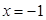 的距离与到点
的距离与到点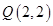 的距离之差的最大值为( )
的距离之差的最大值为( )
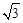
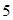

 的顶点在原点,焦点为
的顶点在原点,焦点为 ,动点
,动点 在抛物线
在抛物线 ,则
,则 的最小值为( )
的最小值为( )



 ,则它的焦点坐标是( )
,则它的焦点坐标是( )



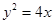 的焦点为F,过点P(2,0)的直线交抛物线于A,B两点,直线AF,BF分别于抛物线交于点C,D.设直线AB,CD的斜率分别为
的焦点为F,过点P(2,0)的直线交抛物线于A,B两点,直线AF,BF分别于抛物线交于点C,D.设直线AB,CD的斜率分别为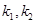 ,则
,则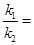 ( )
( )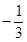 B.
B.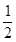 C.1 D.2
C.1 D.2