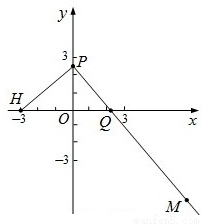
摘要:问题1.已知两点..点在直线上.且. 求点和点的坐标. 问题2.已知.点分的比为.点在线段上.且.求点的坐标. 问题3.已知函数 的图象经过按平移后使得抛物线顶点在轴上.且在轴上截得的弦长为.求平移后函数解析式和. 问题4.定点为圆外一点,为圆上的动点,的平分线交于. 求点的轨迹方程
网址:http://m.1010jiajiao.com/timu_id_4389599[举报]
(1)已知函数f(x)=ax-x(a>1).
①若f(3)<0,试求a的取值范围;
②写出一组数a,x0(x0≠3,保留4位有效数字),使得f(x0)<0成立;
(2)在曲线y=x-
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线y=x+
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(3)当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并取a=
及a=
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间(0,
]上单调递减,在区间[
,1)上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
查看习题详情和答案>>
①若f(3)<0,试求a的取值范围;
②写出一组数a,x0(x0≠3,保留4位有效数字),使得f(x0)<0成立;
(2)在曲线y=x-
| 2 |
| x |
| p |
| x |
(3)当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并取a=
| 1 |
| 16 |
| ||
| 2 |
| 1 |
| e |
| 1 |
| e |
(1)已知函数f(x)=ax-x(a>1).
①若f(3)<0,试求a的取值范围;
②写出一组数a,x(x≠3,保留4位有效数字),使得f(x)<0成立;
(2)在曲线 上存在两个不同点关于直线y=x对称,求出其坐标;若曲线
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线 (p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(3)当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并取 及
及 加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
查看习题详情和答案>>
①若f(3)<0,试求a的取值范围;
②写出一组数a,x(x≠3,保留4位有效数字),使得f(x)<0成立;
(2)在曲线
 上存在两个不同点关于直线y=x对称,求出其坐标;若曲线
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线 (p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;(3)当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并取
 及
及 加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)查看习题详情和答案>>
 (p≠0)上存在两个不同点关于直线y=x对称,求实数p的取值范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的取值范围;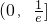 上单调递减,在区间
上单调递减,在区间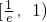 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)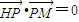 ,
,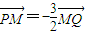 .
.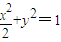 ,并将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解.
,并将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解.