题目内容
如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足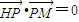 ,
,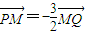 .
.(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过定点F(1,0)作互相垂直的直线l与l',l与(1)中的轨迹C交于A、B两点,l'与(1)中的轨迹C交于D、E两点,求四边形ADBE面积S的最小值;
(3)将(1)中的曲线C推广为椭圆:
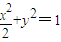 ,并将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解.
,并将(2)中的定点取为焦点F(1,0),求与(2)相类似的问题的解.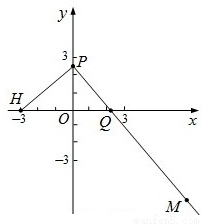
【答案】分析:(1)设出M的坐标,利用题意向量的关系,求得x和y的关系,进而求得M的轨迹C.
(2)将直线l与l'的方程与轨迹C的方程联立,分别求弦长,从而表达出四边形ADBE面积S,再利用基本不等式求最小值;
(3)将直线l与l'的方程与椭圆的方程联立,分别求弦长,从而表达出四边形ADBE面积S,再利用基本不等式求最小值;
解答:解:(1)设M(x,y),P(0,b),Q(a,0)(a≥0),易知 ,
, ,
, ,由题设
,由题设 ,得
,得 其中a≥0,从而
其中a≥0,从而 ,
, ,且x≥0,
,且x≥0,
又由已知 ,得HP⊥PM,
,得HP⊥PM,
当b≠0时,y≠0,此时 ,得
,得 ,
,
又kPM=kPQ,故 ,
, ,
,
即 ,y2=4x(x≠0),
,y2=4x(x≠0),
当b=0时,点P为原点,HP为x轴,PM为y轴,点Q也为原点,从而点M也为原点,因此点M的轨迹C的方程为y2=4x,它表示以原点为顶点,以(1,0)为焦点的抛物线; (4分)
(2)由题设,可设直线l的方程为y=k(x-1)(k≠0),直线l'的方程为 ,(k≠0),又设A(x1,y1)、B(x2,y2),
,(k≠0),又设A(x1,y1)、B(x2,y2),
则由 ,消去x,整理得ky2-4y-4k=0,
,消去x,整理得ky2-4y-4k=0,
故 ,同理|DE|=4(1+k2),(7分)
,同理|DE|=4(1+k2),(7分)
则 ,
,
当且仅当k=±1时等号成立,因此四边形ADBE面积S的最小值为32.
(9分)
(3)当k≠0时可设直线l的方程为y=k(x-1),
由 ,得(1+2k2)x2-4k2x+2k2-2=0,
,得(1+2k2)x2-4k2x+2k2-2=0,
故 ,
, ,(13分)
,(13分) ,
,
当且仅当k2=1时等号成立.(17分)
当k=0时,易知 ,
, ,得
,得 ,
,
故当且仅当k2=1时四边形ADBE面积S有最小值 .(18分)
.(18分)
点评:本题的考点是直线与圆锥曲线的综合运用,主要考查了椭圆的应用,向量的基本性质.考查了学生分析问题和解决问题的能力,考查利用基本不等式求最值问题.
(2)将直线l与l'的方程与轨迹C的方程联立,分别求弦长,从而表达出四边形ADBE面积S,再利用基本不等式求最小值;
(3)将直线l与l'的方程与椭圆的方程联立,分别求弦长,从而表达出四边形ADBE面积S,再利用基本不等式求最小值;
解答:解:(1)设M(x,y),P(0,b),Q(a,0)(a≥0),易知
 ,
, ,
, ,由题设
,由题设 ,得
,得 其中a≥0,从而
其中a≥0,从而 ,
, ,且x≥0,
,且x≥0,又由已知
 ,得HP⊥PM,
,得HP⊥PM,当b≠0时,y≠0,此时
 ,得
,得 ,
,又kPM=kPQ,故
 ,
, ,
,即
 ,y2=4x(x≠0),
,y2=4x(x≠0),当b=0时,点P为原点,HP为x轴,PM为y轴,点Q也为原点,从而点M也为原点,因此点M的轨迹C的方程为y2=4x,它表示以原点为顶点,以(1,0)为焦点的抛物线; (4分)
(2)由题设,可设直线l的方程为y=k(x-1)(k≠0),直线l'的方程为
 ,(k≠0),又设A(x1,y1)、B(x2,y2),
,(k≠0),又设A(x1,y1)、B(x2,y2),则由
 ,消去x,整理得ky2-4y-4k=0,
,消去x,整理得ky2-4y-4k=0,故
 ,同理|DE|=4(1+k2),(7分)
,同理|DE|=4(1+k2),(7分)则
 ,
,当且仅当k=±1时等号成立,因此四边形ADBE面积S的最小值为32.
(9分)
(3)当k≠0时可设直线l的方程为y=k(x-1),
由
 ,得(1+2k2)x2-4k2x+2k2-2=0,
,得(1+2k2)x2-4k2x+2k2-2=0,故
 ,
, ,(13分)
,(13分) ,
,当且仅当k2=1时等号成立.(17分)
当k=0时,易知
 ,
, ,得
,得 ,
,故当且仅当k2=1时四边形ADBE面积S有最小值
 .(18分)
.(18分)点评:本题的考点是直线与圆锥曲线的综合运用,主要考查了椭圆的应用,向量的基本性质.考查了学生分析问题和解决问题的能力,考查利用基本不等式求最值问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知点A(
如图,已知点A(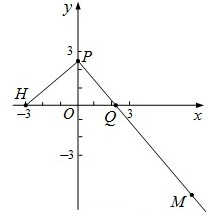 (2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足
(2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足 (2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足
(2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足 ,
, .
. ,并
,并 ,并
,并