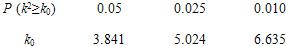摘要:寻求角与角之间的关系.化非特殊角为特殊角, 正确灵活地运用公式.通过三角变换消去或约去一些非特殊角的三角函数值, 一些常规技巧:“ 的代换.切割化弦.和积互化.异角化同角等. 三角函数式的化简常用方法是:异名函数化为同名三角函数.异角化为同角.异次化为同次.切割化弦.特殊值与特殊角的三角函数互化. 三角恒等式的证明: 三角恒等式包括有条件的恒等式和无条件的恒等式. ①无条件的等式证明的基本方法是化繁为简.左右归一.变更命题等.使等式两端的“异 化为“同 ,②有条件的等式常用方法有:代入法.消去法.综合法.分析法等.
网址:http://m.1010jiajiao.com/timu_id_4389539[举报]
为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月人住的游客人数,发现每年各个月份来客栈人住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,人住客栈的游客人数基本相同;
②人住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份人住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
查看习题详情和答案>>
①每年相同的月份,人住客栈的游客人数基本相同;
②人住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份人住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
设数列{an}满足an>0,(n∈N+),其前n项和为Sn,且
+
+
+…+
=
(1)求an+1与Sn之间的关系,并求数列{an}的通项公式;
(2)令Tn=
+
+…+
,求证:
[(1-
)
]<2(
-1)..
查看习题详情和答案>>
| a | 3 1 |
| a | 3 2 |
| a | 3 3 |
| a | 3 n |
| S | 2 n |
(1)求an+1与Sn之间的关系,并求数列{an}的通项公式;
(2)令Tn=
| 1 | ||
a1
|
| 1 | ||
a2
|
| 1 | ||
an
|
| n |
 |
| i=1 |
| Ti |
| Ti+1 |
| 1 | ||
|
| 2 |