摘要:设函数的定义域为.值域为.由求出.如果对于中 每个值.在中都有唯一的值和它对应.那么为以为自变量的函数.叫做的反函数.记作.() 反函数存在的条件:从定义域到值域上的一一映射确定的函数才有反函数, 反函数的定义域.值域上分别是原函数的值域.定义域.若与 互为反函数.函数的定义域为.值域为.则., 互为反函数的两个函数具有相同的单调性.它们的图象关于对称. 一些结论:定义域上的单调函数必有反函数,奇函数若存在反函数.则其反函数也是奇函数,定义域为非单元素集的偶函数不存在反函数.周期函数在整个定义域内不存在反函数.
网址:http://m.1010jiajiao.com/timu_id_4389446[举报]
若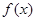 的定义域为
的定义域为 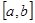 ,值域为
,值域为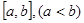 ,则称函数
,则称函数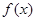 是
是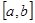 上的“四维方军”函数.
上的“四维方军”函数.
(1)设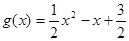 是
是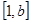 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数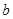 的值;
的值;
(2)问是否存在常数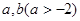 使函数
使函数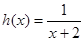 是区间
是区间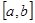 上的“四维方军”函数?若存在,求出
上的“四维方军”函数?若存在,求出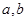 的值,否则,请说明理由.
的值,否则,请说明理由.
查看习题详情和答案>>
若 的定义域为
的定义域为  ,值域为
,值域为 ,则称函数
,则称函数 是
是 上的“四维方军”函数.
上的“四维方军”函数.
(1)设 是
是 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数 的值;
的值;
(2)问是否存在常数 使函数
使函数 是区间
是区间 上的“四维方军”函数?若存在,求出
上的“四维方军”函数?若存在,求出 的值,否则,请说明理由.
的值,否则,请说明理由.
若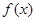 的定义域为
的定义域为 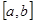 ,值域为
,值域为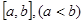 ,则称函数
,则称函数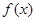 是
是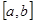 上的“四维方军”函数.
上的“四维方军”函数.
(1)设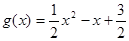 是
是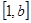 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数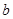 的值;
的值;
(2)问是否存在常数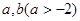 使函数
使函数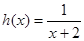 是区间
是区间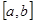 上的“四维方军”函数?若存在,求出
上的“四维方军”函数?若存在,求出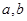 的值,否则,请说明理由.
的值,否则,请说明理由.
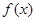 的定义域为
的定义域为 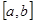 ,值域为
,值域为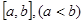 ,则称函数
,则称函数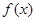 是
是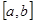 上的“四维方军”函数.
上的“四维方军”函数.(1)设
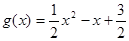 是
是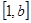 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数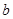 的值;
的值;(2)问是否存在常数
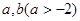 使函数
使函数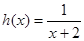 是区间
是区间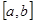 上的“四维方军”函数?若存在,求出
上的“四维方军”函数?若存在,求出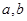 的值,否则,请说明理由.
的值,否则,请说明理由.