摘要：7．有8张卡片分别标有数字1,2,3,4,5,6,7,8.从中取出6张卡片排成3行2列.要求3行中仅有中间行的两张卡片上的数字之和为5.则不同的排法共有( ) A．1344种 B．1248种 C．1056种 D．960种 答案:B 解析:中间行两张卡片为1,4或2,3.且另两行不可同时出现这两组数字．①用间接法.先写出中间行为.C·A·A,②去掉两行同时出现1,4或2,3.(AC)2A.所以CAA-(AC)2A＝1440-192＝1248.故选B.
网址：http://m.1010jiajiao.com/timu_id_4388446[举报]
（2008•浦东新区二模）已知等差数列{xn}，Sn是{xn}的前n项和，且x3=5，S5+x5=34．
（1）求{xn}的通项公式；
（2）设an=(
)n，Tn是{an}的前n项和，方程Sn+Tn=2008是否有解？说明理由；
（3）是否存在正数λ，对任意的正整数n，不等式λxn-4Sn＜228恒成立？若存在，求出λ的取值范围；若不存在，说明理由．
查看习题详情和答案>>
（1）求{xn}的通项公式；
（2）设an=(
| 1 | 3 |
（3）是否存在正数λ，对任意的正整数n，不等式λxn-4Sn＜228恒成立？若存在，求出λ的取值范围；若不存在，说明理由．
已知等差数列{xn}，Sn是{xn}的前n项和，且x3=5，S5+x5=34．
（1）求{xn}的通项公式；
（2）设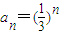
，Tn是{an}的前n项和，方程Sn+Tn=2008是否有解？说明理由；
（3）是否存在正数λ，对任意的正整数n，不等式λxn-4Sn＜228恒成立？若存在，求出λ的取值范围；若不存在，说明理由．
查看习题详情和答案>>
（1）求{xn}的通项公式；
（2）设
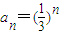，Tn是{an}的前n项和，方程Sn+Tn=2008是否有解？说明理由；（3）是否存在正数λ，对任意的正整数n，不等式λxn-4Sn＜228恒成立？若存在，求出λ的取值范围；若不存在，说明理由．
查看习题详情和答案>>
某市2008年底有住房面积1 200万平方米，计划从2009年起，每年拆除20万平方米的旧住房．假定该市每年新建住房面积是上年年底住房面积的
．
(1)分别求2009年底和2010年底的住房面积；
(2)求2028年底的住房面积．(计算结果以万平方米为单位，且精确到0.01)
查看习题详情和答案>>
；②展开式中非常数项的系数和为一1；