题目内容
已知等差数列{xn},Sn是{xn}的前n项和,且x3=5,S5+x5=34.(1)求{xn}的通项公式;
(2)设
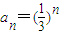 ,Tn是{an}的前n项和,方程Sn+Tn=2008是否有解?说明理由;
,Tn是{an}的前n项和,方程Sn+Tn=2008是否有解?说明理由;(3)是否存在正数λ,对任意的正整数n,不等式λxn-4Sn<228恒成立?若存在,求出λ的取值范围;若不存在,说明理由.
【答案】分析:(1)由x3=5,S5+x5=34,能推导出x1=1,d=2,由此能求出{xn}的通项公式.
(2)由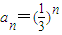 ,知
,知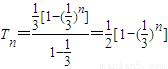 ,所以
,所以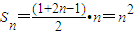 ,则方程Sn+Tn=2008为:
,则方程Sn+Tn=2008为: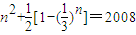 .由此能导出方程Sn+Tn=2008无解.
.由此能导出方程Sn+Tn=2008无解.
(3)λ(2n-1)-4n2<228,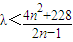 .由于
.由于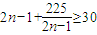 ,所以0<λ<28.
,所以0<λ<28.
解答:解:(1)由x3=5,S5+x5=34,
所以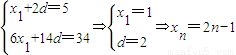 ------------------------------------------(4分)
------------------------------------------(4分)
(2)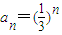 ,则
,则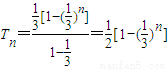 ---(5分)
---(5分) 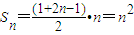 --(6分)
--(6分)
则方程Sn+Tn=2008为: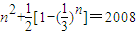
令: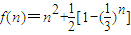 ,则f(n)单调递增----------------------------------------(8分)
,则f(n)单调递增----------------------------------------(8分)
当n≤44时,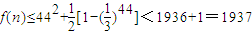
当n≥45时,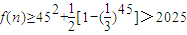 所以方程无解.---------------(10分)
所以方程无解.---------------(10分)
(3)λ(2n-1)-4n2<228,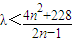 -------------------------------------------(12分)
-------------------------------------------(12分)
即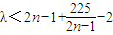 ----------------------------------------------------------------(14分),
----------------------------------------------------------------(14分),
由于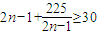 ,所以0<λ<28--------------------------------------------(16分)
,所以0<λ<28--------------------------------------------(16分)
点评:本题考查数列与不等式的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
(2)由
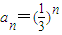 ,知
,知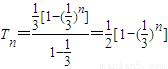 ,所以
,所以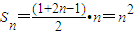 ,则方程Sn+Tn=2008为:
,则方程Sn+Tn=2008为: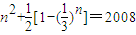 .由此能导出方程Sn+Tn=2008无解.
.由此能导出方程Sn+Tn=2008无解.(3)λ(2n-1)-4n2<228,
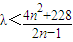 .由于
.由于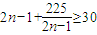 ,所以0<λ<28.
,所以0<λ<28.解答:解:(1)由x3=5,S5+x5=34,
所以
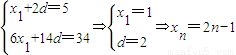 ------------------------------------------(4分)
------------------------------------------(4分)(2)
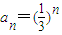 ,则
,则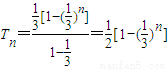 ---(5分)
---(5分) 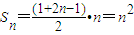 --(6分)
--(6分)则方程Sn+Tn=2008为:
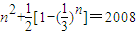
令:
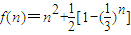 ,则f(n)单调递增----------------------------------------(8分)
,则f(n)单调递增----------------------------------------(8分)当n≤44时,
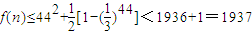
当n≥45时,
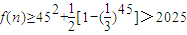 所以方程无解.---------------(10分)
所以方程无解.---------------(10分)(3)λ(2n-1)-4n2<228,
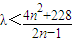 -------------------------------------------(12分)
-------------------------------------------(12分)即
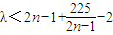 ----------------------------------------------------------------(14分),
----------------------------------------------------------------(14分),由于
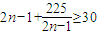 ,所以0<λ<28--------------------------------------------(16分)
,所以0<λ<28--------------------------------------------(16分)点评:本题考查数列与不等式的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
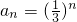 ,Tn是{an}的前n项和,是否存在正数λ,对任意正整数n,k,不等式
,Tn是{an}的前n项和,是否存在正数λ,对任意正整数n,k,不等式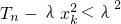 恒成立?若存在,求λ的取值范围;若不存在,说明理由.
恒成立?若存在,求λ的取值范围;若不存在,说明理由.