摘要：2．已知一个直角三角形的三边分别为3.4.5.利用面积公式设计一个算法.求出它的面积.并画出算法的程序框图. 算法分析:这是一个简单的问题.只需将两直角边的数值代入公式.最后输出结果. 程序框图:
网址：http://m.1010jiajiao.com/timu_id_4386855[举报]
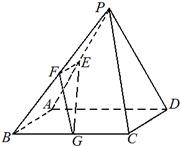已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E、F、G分别是PA、PB、BC的中点．（1）求证：EF⊥平面PAD；
（2）求平面EFG与平面ABCD所成锐二面角的大小；
（3）若M为线段AB上靠近A的一个动点，问当AM长度等于多少时，直线MF与平面EFG所成角的正弦值等于
| ||
| 5 |
一个三棱锥的三视图如图所示，其中正视图和侧视图是两条直角边分别是1和2的两个全等的直角三角形，俯视图是直角边长为1的等腰直角三角形．（Ⅰ）请画出这个三棱锥的直观图，并求出它的体积；
（Ⅱ）以D为顶点，DD1，DA，DC为相邻的三条棱，作
平行六面体ABCD-A1B1C1D1，已知点E在AA1上移动
（1）当E点为AA1的中点时，证明BE⊥平面B1C1E．
（2）在CC1上求一点P，使得平面BC1E∥平面PAD1，指出P点的位置
（Ⅲ）AE为何值时，二面角C-ED1-D的大小为45°． 查看习题详情和答案>>
已知双曲线S的两个焦点F1、F2在x轴上，它的两条渐近线分别为l1、l2，y=
x是其中的一条渐近线的方程，两条直线X=±
是双曲线S的准线．
（I）设A、B分别为l1、l2上的动点，且2|
|=5
，求线段AB的中点M的轨迹方程：
（II）已知O是原点，经过点N（0，1）是否存在直线l，使l与双曲线S交于P，E且△POE是以PE为斜边的直角三角形？若存在，求出直线l的方程；若不存在，请说明理由． 查看习题详情和答案>>
| ||
| 3 |
| 3 |
| 2 |
（I）设A、B分别为l1、l2上的动点，且2|
| AB |
| F1F2 |
（II）已知O是原点，经过点N（0，1）是否存在直线l，使l与双曲线S交于P，E且△POE是以PE为斜边的直角三角形？若存在，求出直线l的方程；若不存在，请说明理由． 查看习题详情和答案>>