摘要：问5分. 已知以原点为中心的椭圆的一条准线方程为.离心率.是椭圆上的动点． (Ⅰ)若的坐标分别是.求的最大值, 图.点的坐标为.是圆上的点.是点在轴上的射影.点满足条件:.．求线段的中点的轨迹方程, 21世纪教育网 解:(Ⅰ)由题设条件知焦点在y轴上.故设椭圆方程为. 设.由准线方程得.由得.解得 a = 2 ,c = .从而 b = 1.椭圆方程为 . 又易知C.D两点是椭圆的焦点.所以, 从而.当且仅当.即点M的坐标为 时上式取等号.的最大值为4 . 21世纪教育网 图.设 .因为.故 ① 因为 所以 . ② 记P点的坐标为.因为P是BQ的中点 所以 由因为 .结合①.②得 21世纪教育网 故动点P的估计方程为
网址：http://m.1010jiajiao.com/timu_id_4383913[举报]
（2009重庆卷理）（本小题满分12分，（Ⅰ）问5分，（Ⅱ）问7分）
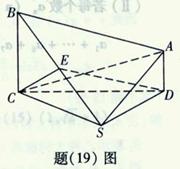
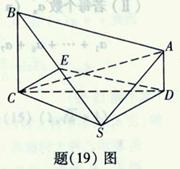
如题（19）图，在四棱锥
中，
且
；平面
平面
，
；
为
的中点，
．求：
（Ⅰ）点
到平面
的距离；
（Ⅱ）二面角
的大小． .
（2009重庆卷理）（本小题满分12分，（Ⅰ）问5分，（Ⅱ）问7分）
设
个不全相等的正数
依次围成一个圆圈．
（Ⅰ）若
，且
是公差为
的等差数列，而
是公比为
的等比数列；数列
的前
项和
满足：
，求通项
；
（Ⅱ）若每个数是其左右相邻两数平方的等比中项，求证：
；
中，
且
；平面
平面
，
；
为
的中点，
．求：
到平面
的距离；
的大小． . 
为中心的椭圆的一条准线方程为
，离心率
，
是椭圆上的动点．
的坐标分别是
，求
的最大值；
的坐标为
，
是圆
上的点，
是点
轴上的射影，点
满足条件：
，
．求线段
的中点
的轨迹方程；