摘要：本题共有3个小题.第1小题满分4分.第2小题满分4分.第3小题满分8分. 已知双曲线C的中心是原点.右焦点为F.一条渐近线m:,设过点A的直线l的方向向量. (1) 求双曲线C的方程, (2) 若过原点的直线.且a与l的距离为.求K的值, (3) 证明:当时.在双曲线C的右支上不存在点Q.使之到直线l的距离为. [解](1)设双曲线的方程为 .解额双曲线的方程为 (2)直线.直线 由题意.得.解得 (3)[证法一]设过原点且平行于的直线 则直线与的距离当时. 21世纪教育网 又双曲线的渐近线为 双曲线的右支在直线的右下方. 双曲线右支上的任意点到直线的距离大于. 故在双曲线的右支上不存在点.使之到直线的距离为 [证法二]假设双曲线右支上存在点到直线的距离为. 则 由(1)得 设. 当时., 将代入(2)得 . 方程不存在正根.即假设不成立. 故在双曲线的右支上不存在点.使之到直线的距离为 21世纪教育网
网址：http://m.1010jiajiao.com/timu_id_4383912[举报]
（2009上海卷文）（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分 .
已知ΔABC的角A、B、C所对的边分别是a、b、c，设向量
，
，
.
若
//
，求证：ΔABC为等腰三角形；
若⊥
，边长c = 2，角C = 
，求ΔABC的面积 .
（2009上海卷文）（本题满分18分）本题共有3个小题，第1小题满分5分，第2小题满分5分，第3小题满分8分.
已知
是公差为d的等差数列，
是公比为q的等比数列
（1）若 
，是否存在
，有
？请说明理由；
（2）若
（a、q为常数，且aq
0）对任意m存在k，有
，试求a、q满足的充要条件；
（3）若
试确定所有的p,使数列中存在某个连续p项的和式数列中的一项，请证明.
，
，
.
//
，求证：ΔABC为等腰三角形； 
，边长c = 2，角C = 
，求ΔABC的面积 .
表示某学科知识的学习次数（
），
表示对该学科知识的掌握程度，正实数a与学科知识有关．
7时，掌握程度的增长量f（x+1）－ f(x)总是下降；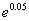 
＝1．0513）