19（本小题满分14分）已知，函数，（其中为自然对数的底数）．（1）求函数在区间上的最小值；（2）是否存在实数，使曲线在点处的切线与轴垂直? 若存在，求出的值；若不存在，请说明理由．

2009全国卷Ⅱ理（本小题满分12分）

某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽取3名工人进行技术考核。

（I）求从甲、乙两组各抽取的人数；     

（II）求从甲组抽取的工人中恰有1名女工人的概率；

（III）记表示抽取的3名工人中男工人数，求的分布列及数学期望。              

 19（本小题满分12分）

P是以为焦点的双曲线C：（a＞0，b＞0）上的一点，已知=0，．

（1）试求双曲线的离心率；

（2）过点P作直线分别与双曲线两渐近线相交于P₁、P₂两点，当，= 0，求双曲线的方程．

19（本小题满分13分）

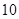随机抽取某中学甲乙两班各名同学,测量他们的身高(单位: 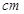),获得身高数据的茎叶图如下图：

(1)根据茎叶图判断哪个班的平均身高较高；

(2)计算甲班的样本方差；

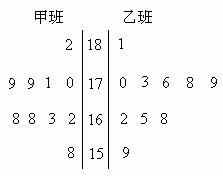(3)现从乙班这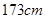名同学中随机抽取两名身高不低于的同学,求身高为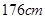的同学被抽中的概率。

19（本小题满分14分）已知f(x)＝2^x－1的反函数为(x)，g(x)＝log₄(3x＋1)．(1)若f^－1(x)≤g(x)，求x的取值范围D；(2)设函数H(x)＝g(x)－(x)，当x∈D时，求函数H(x)的值域．