摘要：利用三角函数的有界性如|sinx|≤1.|cosx|≤1来求三角函数的最值 例2 a.b是不相等的正数 求y＝的最大值和最小值 解:y是正值.故使y2达到最大的x值也使y达到最大 y2＝acos2x+bsin2x+2·+asin2x+bcos2x ＝a+b+ ∵a≠b.(a-b)2＞0.0≤sin22x≤1 ∴当sin2x＝±1时.即x＝(k∈Z)时.y有最大值, 当sinx＝0时.即x＝ (k∈Z)时.y有最小值+
网址：http://m.1010jiajiao.com/timu_id_4382011[举报]
（本题满分12分）已知函数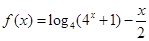
．
(1)判断f(x)的奇偶性，并说明理由；
(2)若方程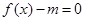
有解，求m的取值范围；
【解析】第一问利用函数的奇偶性的定义可以判定定义域和f(x)与f(-x)的关系从而得到结论。
第二问中，利用方程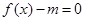有解，说明了参数m落在函数y=f(x)的值域里面即可。
查看习题详情和答案>>
已知数列{an}满足an=
.
. （1）试比较an与an+1的大小.
（2）an=(n+1)(
)n，试判断此数列的增减性和有界性.
（3）在(2)中有无最大项?若有，求出最大项和最大项项数；若没有，说明理由.
查看习题详情和答案>>函数
在同一个周期内，当
时,
取最大值1，当
时，取最小值
。
（1）求函数的解析式
（2）函数
的图象经过怎样的变换可得到
的图象？
（3）若函数
满足方程
求在
内的所有实数根之和.
【解析】第一问中利用
又因
又
函数
第二问中，利用的图象向右平移
个单位得
的图象
再由
图象上所有点的横坐标变为原来的
.纵坐标不变，得到
的图象，
第三问中，利用三角函数的对称性，
的周期为
在内恰有3个周期，
并且方程
在内有6个实根且
同理，
可得结论。
解：(1)
又因
又 函数
(2)的图象向右平移个单位得的图象
再由图象上所有点的横坐标变为原来的.纵坐标不变，得到的图象，
(3)的周期为
在内恰有3个周期，
并且方程在内有6个实根且
同理，
故所有实数之和为
查看习题详情和答案>>
．
，矩形的面积设为S，则
＝
．
时，S有最大值，即此时矩形的面积最大．