摘要:20. 已知点在直线上.点--.顺次为轴上的点,其中.对于任意.点构成以为顶角的等腰三角形, 设的面积为. (1)证明:数列是等差数列, (2)求(用和的代数式表示), (3)设数列前项和为.判断与()的大小.并证明你的结论, 解:(1)由于点在直线上. 则. 因此.所以数列是等差数列 (2)由已知有.那么 同理 以上两式相减.得. ∴成等差数列,也成等差数列. ∴. 点.则.. 而 ∴ 得:. 则 而.则. 即 ∴ ∴ ∴ 由于 . 而, 则, 从而 , 同理: -- 以上个不等式相加得: 即. 从而 .
网址:http://m.1010jiajiao.com/timu_id_4381852[举报]
(本小题满分14分)已知A(8,0),B、C两点分别在y轴和x轴上运动,并且满足![]() 。
。
(1)求动点P的轨迹方程。
(2)若过点A的直线L与动点P的轨迹交于M、N两点,且![]()
其中Q(-1,0),求直线L的方程.
查看习题详情和答案>>(本小题满分14分)
已知抛物线、椭圆、双曲线都经过点M(1,2),它们在x轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线方程;
(Ⅱ)若定点P(3,0),A为抛物线上任意一点,是否存在垂直于x轴的直线l被以AP为直径的圆截得的弦长为定值?若存在,求出l的方程;若不存在,说明理由。
查看习题详情和答案>>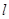 :
: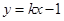 与圆
与圆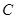 :
: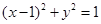 相交于
相交于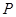 、
、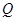 两点,点
两点,点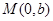 满足
满足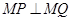 .
.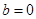 时,求实数
时,求实数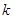 的值;
的值;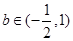 时,求实数
时,求实数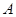 、
、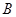 是圆
是圆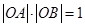 ,试问:是否存在一个定圆
,试问:是否存在一个定圆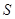 ,使直线
,使直线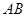 恒与圆
恒与圆 .
. ,曲线
,曲线 和
和 在原点处的切线重合,求实数
在原点处的切线重合,求实数 的值.
的值. ,
,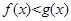 在
在 上恒成立,求
上恒成立,求 ,在
,在 图象与直线y=1是否有交点?若有,求出交点,若没有,请说明理由.
图象与直线y=1是否有交点?若有,求出交点,若没有,请说明理由.