摘要:3.数学思想 (1)迭加累加(等差数列的通项公式的推导方法)若.则--, (2)迭乘累乘(等比数列的通项公式的推导方法)若.则--, (3)逆序相加(等差数列求和公式的推导方法), (4)错位相减(等比数列求和公式的推导方法).
网址:http://m.1010jiajiao.com/timu_id_4379285[举报]
(2013•福建)当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…=
两边同时积分得:
1dx+
xdx+
x2dx+…
xndx+…=
dx
从而得到如下等式:1×
+
×(
)2+
×(
)3+…+
×(
)n+1+…=ln2.
请根据以上材料所蕴含的数学思想方法,计算:
×
+
×(
)2+
×(
)3+…+
×(
)n+1=
[(
)n+1-1]
[(
)n+1-1].
查看习题详情和答案>>
| 1 |
| 1-x |
两边同时积分得:
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| 1 |
| 1-x |
从而得到如下等式:1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
请根据以上材料所蕴含的数学思想方法,计算:
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
已知函数 ,
, ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
【解析】本试题考查了运用导数来研究函数的单调性,并求解参数的取值范围。与此同时还能对于方程解的问题,转化为图像与图像的交点问题来长处理的数学思想的运用。
查看习题详情和答案>>
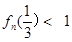 .
.
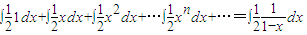
 .
. = .
= .