摘要: 导数法 [典型例题] [例1] 求下列函数值域 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) 答案: (1) (2) (3) (4) (5) (6) (7) (8) ∴ (9) (10) 且 且 且 (11)令 (12)令 (13)令 ∴ (14) ① ② 且 ∴ (15) (16)P()A ∴ ∴ (17) ∴ ∴ ∴ (18) 令 ∴ ∴ [例2] .为方程的两根.为何值时.最小.并求最小值. 答案: ∴ 时. [例3] ...求的最值. 答案: ∴ [模拟试题]
网址:http://m.1010jiajiao.com/timu_id_4378331[举报]
我们把形如y=f(x
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得lny=lnf(x
=φ(x)lnf(x),两边对x求导数,得
=φ′(x)lnf(x)+φ(x)
,于是y′=f(x
[φ′(x)lnf(x)+φ(x)
],运用此方法可以求得函数y=
(x>0)在(1,1)处的切线方程是
查看习题详情和答案>>
| ) | φ(x) |
| ) | φ(x) |
| y′ |
| y |
| f′(x) |
| f(x) |
| ) | φ(x) |
| f′(x) |
| f(x) |
| x | x |
y=x
y=x
.我们把形如y=f(x)φ(x)的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得lny=φ(x)lnf(x),两边求导数,得
=φ′(x)lnf(x)+φ(x)
,于是y′=f(x)φ(x)[φ′(x)lnf(x)+φ(x)
],运用此方法可以探求得函数y=x
的一个单调递增区间是( )
| y′ |
| y |
| f′(x) |
| f(x) |
| f′(x) |
| f(x) |
| 1 |
| x |
函数y=f(x)g(x)在求导数时,可以运用对数法:在函数解析式两边求对数得lny=g(x)lnf(x),两边求导数
=g′(x)lnf(x)+g(x)
,于是y'=f(x)g(x)[g′(x)lnf(x)+g(x)
].运用此方法可以探求得知y=x
(x>0)的一个单调增区间为 .
查看习题详情和答案>>
| y′ |
| y |
| f′(x) |
| f(x) |
| f′(x) |
| f(x) |
| 1 |
| x |
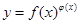 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得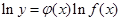 ,两边求导数,得
,两边求导数,得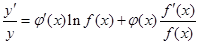 ,于是
,于是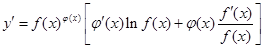 ,运用此方法可以探求得函数
,运用此方法可以探求得函数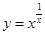 的一个单调递增区间是
的一个单调递增区间是
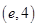 B.
B.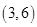 C.
C.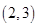 D.
D. 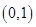
 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得 ,两边对x求导数,得
,两边对x求导数,得 于是
于是 ,运用此方法可以求得函数
,运用此方法可以求得函数 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .