摘要:(1)椭圆的定义:平面内与两个定点的距离的和等于常数(大于)的点的轨迹. 第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数的点的轨迹. 其中:两个定点叫做椭圆的焦点.焦点间的距离叫做焦距,定直线叫做准线. 常数叫做离心率. 注意:表示椭圆,表示线段,没有轨迹, (2)椭圆的标准方程.图象及几何性质: 中心在原点.焦点在轴上 中心在原点.焦点在轴上 标准方程 参数方程 为参数) 为参数) 图 形 A1 顶 点 对称轴 轴.轴,短轴为.长轴为 焦 点 焦 距 离心率 准 线 通 径 (为焦准距) 焦半径 焦点弦 仅与它的中点的横坐标有关 仅与它的中点的纵坐标有关 焦准距
网址:http://m.1010jiajiao.com/timu_id_4377357[举报]
椭圆 的左、右焦点分别为
的左、右焦点分别为 ,一条直线
,一条直线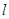 经过点
经过点 与椭圆交于
与椭圆交于 两点.
两点.
⑴求 的周长;
的周长;
⑵若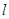 的倾斜角为
的倾斜角为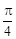 ,求
,求 的面积.
的面积.
【解析】(1)根据椭圆的定义 的周长等于4a.
的周长等于4a.
(2)设 ,则
,则 ,然后直线l的方程与椭圆方程联立,消去x,利用韦达定理可求出所求三角形的面积.
,然后直线l的方程与椭圆方程联立,消去x,利用韦达定理可求出所求三角形的面积.
查看习题详情和答案>>
已知椭圆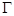 :
: .
.

(1)椭圆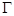 的短轴端点分别为
的短轴端点分别为 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆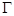 交于
交于 两点,其中点
两点,其中点 满足
满足 ,且
,且 .
.
①证明直线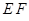 与
与 轴交点的位置与
轴交点的位置与 无关;
无关;
②若∆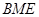 面积是∆
面积是∆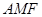 面积的5倍,求
面积的5倍,求 的值;
的值;
(2)若圆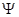 :
: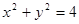 .
. 是过点
是过点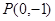 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆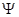 于
于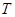 、
、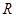 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 .求
.求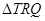 面积取最大值时直线
面积取最大值时直线 的方程.
的方程.
查看习题详情和答案>>
(本小题共13分)
已知椭圆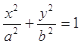
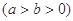 和直线L:
和直线L: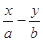 =1, 椭圆的离心率
=1, 椭圆的离心率 ,直线L与坐标原点的距离为
,直线L与坐标原点的距离为 。
。
(1)求椭圆的方程;
(2)已知定点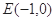 ,若直线
,若直线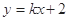
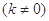 与椭圆相交于C、D两点,试判断是否存在
与椭圆相交于C、D两点,试判断是否存在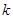 值,使以CD为直径的圆过定点E?若存在求出这个
值,使以CD为直径的圆过定点E?若存在求出这个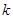 值,若不存在说明理由。
值,若不存在说明理由。
查看习题详情和答案>>
 的右焦点
的右焦点 ,其右准线与
,其右准线与 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点 (B)
(B) (C)
(C)  (D)
(D)
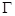 :
: .
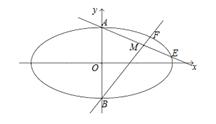
.
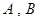 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆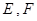 两点,其中点
两点,其中点 满足
满足 ,且
,且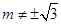 .
. 与
与 轴交点的位置与
轴交点的位置与 无关;
无关; 面积是∆
面积是∆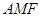 面积的5倍,求
面积的5倍,求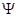 :
: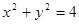 .
.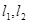 是过点
是过点 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆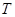 、
、 两点,
两点,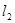 交椭圆
交椭圆 .求
.求 面积取最大值时直线
面积取最大值时直线