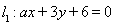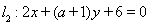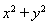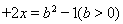摘要:直线与圆的位置关系:直线和圆 有相交.相离.相切.可从代数和几何两个方面来判断: (1)代数方法(判断直线与圆方程联立所得方程组的解的情况):相交, 相离,相切, (2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为.则相交,相离,相切. 提醒:判断直线与圆的位置关系一般用几何方法较简捷. 如(1)圆与直线.的位置关系为 , (2)若直线与圆切于点.则的值 , (3)直线被曲线所截得的弦长等于 , 出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 , (5)已知圆C:.直线L:.①求证:对.直线L与圆C总有两个不同的交点,②设L与圆C交于A.B两点.若.求L的倾斜角,③求直线L中.截圆所得的弦最长及最短时的直线方程.
网址:http://m.1010jiajiao.com/timu_id_4377280[举报]
若直线mx+ny=4和⊙O:x2+y2=4相交,则点P(m,n)与椭圆C:
+
=1的位置关系为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、点P在椭圆C内 |
| B、点P在椭圆C上 |
| C、点P在椭圆C外 |
| D、以上三种均有可能 |