摘要：8．若函数f(x)＝log2的定义域和值域均为[1.+∞).则实数a的取值集合为( ) A．{0} B．{a|0≤a≤1} C．{a|a≥0} D．{a|a≥2} 答案:A 解析:由题意得.log2≥1在x≥1时恒成立.即≥2在x≥1时恒成立, 而≥2即x++a≥2.函数g(x)＝x++a在[1.+∞)上为增函数, ∴g(x)≥g(1)＝1+1+a≥2恒成立.∴a≥0. 由g(x)在[1.+∞)上为增函数.可知f(x)在[1.+∞)也为增函数.∴f(1)＝1.∴a＝0.选A.
网址：http://m.1010jiajiao.com/timu_id_4377060[举报]
（2009•聊城二模）已知函数f(x)=lnx+
，其中a为大于零的常数．
（1）若函数f（x）在区间[1，+∞）内调递增，求a的取值范围；
（2）求函数f（x）在区间[1，2]上的最小值；
（3）求证：对于任意的n∈N*，且n＞1时，都有lnn＞
+
+…+
成立．
查看习题详情和答案>>
| 1-x |
| ax |
（1）若函数f（x）在区间[1，+∞）内调递增，求a的取值范围；
（2）求函数f（x）在区间[1，2]上的最小值；
（3）求证：对于任意的n∈N*，且n＞1时，都有lnn＞
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
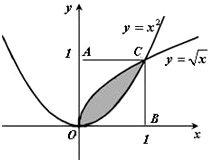（2009•枣庄一模）如图所示，在一个边长为1的正方形AOBC内，曲线y=x2和曲线y=| x |
当前环境问题已成为世界关注的焦点，2009年哥本哈根世界气候大会召开后，为减少汽车尾气对城市的污染，某市决定对出租车实行使用液化气代替汽油的改装工程，原因是液化气燃烧后几乎不产生二氧化碳、一氧化碳、一氧化氮等有害气体，达到减排效果．请根据以下数据：①当前汽油价格为3.8元/升，市内出租车耗油情况是一升汽油能跑11.4千米；②当前液化气价格为4元/升，市内出租车耗油情况是一升液化气能跑16千米；③假设出租车每天能跑240千米．
（Ⅰ）从经济角度衡量一下使用液化气和使用汽油哪一种更经济（即省钱）；
（Ⅱ）假设出租车改装成液化气设备需花费5000元，请问多长时间省出的钱等于改装设备花费的钱． 查看习题详情和答案>>
（Ⅰ）从经济角度衡量一下使用液化气和使用汽油哪一种更经济（即省钱）；
（Ⅱ）假设出租车改装成液化气设备需花费5000元，请问多长时间省出的钱等于改装设备花费的钱． 查看习题详情和答案>>