摘要：6．(人教A版115复习参考题A组第2题) 已知集合..求. 变式1:已知A={x|x3+3x2+2x＞0}.B={x|x2+ax+b≤0}且A∩B={x|0＜x≤2}.A∪B＝{x|x＞-2}.求a.b的值 解:A={x|-2＜x＜-1或x＞0}. 设B=［x1.x2］.由A∩B=(0.2］知x2＝2. 且-1≤x1≤0. ① 由A∪B=知-2≤x1≤-1 ② 由①②知x1＝-1.x2＝2. ∴a＝-(x1+x2)＝-1.b＝x1x2＝-2 设计意图:一元二次不等式与集合的运算综合. 变式2:解关于x的不等式 解:下面对参数m进行分类讨论: ①当m=时.原不等式为x+1>0.∴不等式的解为 ②当时.原不等式可化为 .∴不等式的解为或 ③当时.原不等式可化为 . 当时.原不等式的解集为, 当时.原不等式的解集为, 当时.原不等式无解 综上述.原不等式的解集情况为: ①当时.解为, ②当时.无解, ③当时.解为, ④当m=时.解为, ⑤当时.解为或 设计意图:含参数的一元二次不等式的解法.
网址：http://m.1010jiajiao.com/timu_id_4375447[举报]
某市举行一次数学新课程骨干培训活动，共邀请15名使用不同版本教材的数学教师，具体情况数据如下表所示：
现从这15名教师中随机选出2名，则2人恰好是教不同版本的女教师的概率是
．且a＞b．
（1）求实数a，b的值
（2）培训活动现随机选出2名代表发言，设发言代表中使用人教B版的女教师人数为ξ，求随机变量ξ的分布列和数学期望E（ξ）．
查看习题详情和答案>>
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 | a | 4 | b |
| 2 |
| 35 |
（1）求实数a，b的值
（2）培训活动现随机选出2名代表发言，设发言代表中使用人教B版的女教师人数为ξ，求随机变量ξ的分布列和数学期望E（ξ）．
（2012•自贡三模）某教研机构准备举行一次高中数学新课程研讨会，拟邀请50名使用不同版本的一线教师参加，使用不同版本教材的教师人数如下表所示：
（I）从这50名教师中随机选出2名教师发言，求第一位发言的教师所使用版本是北大师大版的概率；
（II ）设使用北师大版的5名教师中有3名男教师，2名女教师，若随机选出2名用北师大版的教师发言，求抽到男教师个数的分布列和期望．
查看习题详情和答案>>
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 10 | 5 |
（II ）设使用北师大版的5名教师中有3名男教师，2名女教师，若随机选出2名用北师大版的教师发言，求抽到男教师个数的分布列和期望．
某研究机构准备举行一次数学新课程研讨会，共邀请50名一线教师参加，使用不同版本教材的教师人数如下表所示：
（1）从这50名教师中随机选出2名，求2人所使用版本相同的概率；
（2）若随机选出2名使用人教版的教师发言，设使用人教A版的教师人数为ξ，求随机变量ξ的变分布列和数学期望． 查看习题详情和答案>>
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 5 | 10 |
（2）若随机选出2名使用人教版的教师发言，设使用人教A版的教师人数为ξ，求随机变量ξ的变分布列和数学期望． 查看习题详情和答案>>
某市举行的一次数学新课程骨干培训，共邀请15名使用不同版本教材的教师，数据如下表所示：
（Ⅰ）从这15名教师中随机选出2名，则2人恰好是教不同版本的男教师的概率是多少？
（Ⅱ）培训活动随机选出2名代表发言，设发言代表中使用人教B版的女教师人数为ξ，求随机变量ξ的分布列和数学期望Eξ． 查看习题详情和答案>>
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 | 3 | 4 | 2 |
（Ⅱ）培训活动随机选出2名代表发言，设发言代表中使用人教B版的女教师人数为ξ，求随机变量ξ的分布列和数学期望Eξ． 查看习题详情和答案>>
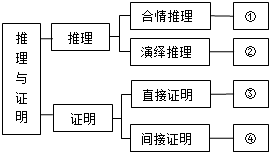4、如图是人教A版教材选修1-2第二章“推理与证明”的知识结构图（部分），如果要加入知识点“三段论”，则应该放在图中（ ）