摘要：已知向量.,向量与平行,︱︱=4则向量的坐标是 ◆例题答案:1-3.DBD;
网址：http://m.1010jiajiao.com/timu_id_4374193[举报]
（2010•上海）在平面上，给定非零向量
，对任意向量
，定义
=
-
．
（1）若
=（2，3），
=（-1，3），求
；
（2）若
=（2，1），证明：若位置向量
的终点在直线Ax+By+C=0上，则位置向量
的终点也在一条直线上；
（3）已知存在单位向量
，当位置向量
的终点在抛物线C：x2=y上时，位置向量
终点总在抛物线C′：y2=x上，曲线C和C′关于直线l对称，问直线l与向量
满足什么关系？
查看习题详情和答案>>
| b |
| a |
| a′ |
| a |
2(
| ||||
|
|
| b |
（1）若
| a |
| b |
| a′ |
（2）若
| b |
| a |
| a′ |
（3）已知存在单位向量
| b |
| a |
| a′ |
| b |
在平面上，给定非零向量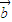
，对任意向量
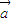，定义
=
-
．
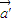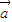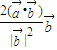（1）若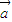
=（2，3），
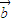=（-1，3），求
；
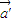（2）若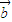
=（2，1），证明：若位置向量
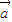的终点在直线Ax+By+C=0上，则位置向量
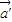的终点也在一条直线上；
（3）已知存在单位向量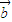
，当位置向量
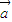的终点在抛物线C：x2=y上时，位置向量
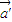终点总在抛物线C′：y2=x上，曲线C和C′关于直线l对称，问直线l与向量
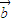满足什么关系？
查看习题详情和答案>>
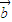，对任意向量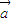，定义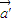=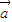-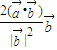．（1）若
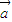=（2，3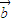），=（-1，3），求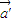；（2）若
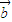=（2，1），证明：若位置向量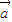的终点在直线Ax+By+C=0上，则位置向量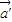的终点也在一条直线上；（3）已知存在单位向量
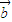，当位置向量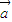的终点在抛物线C：x2=y上时，位置向量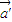终点总在抛物线C′：y2=x上，曲线C和C′关于直线l对称，问直线l与向量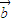满足什么关系？查看习题详情和答案>>
在平面上，给定非零向量
，对任意向量
，定义
=
-
．
（1）若
=（2，3），
=（-1，3），求
；
（2）若
=（2，1），证明：若位置向量
的终点在直线Ax+By+C=0上，则位置向量
的终点也在一条直线上；
（3）已知存在单位向量
，当位置向量
的终点在抛物线C：x2=y上时，位置向量
终点总在抛物线C′：y2=x上，曲线C和C′关于直线l对称，问直线l与向量
满足什么关系？
查看习题详情和答案>>
| b |
| a |
| a′ |
| a |
2(
| ||||
|
|
| b |
（1）若
| a |
| b |
| a′ |
（2）若
| b |
| a |
| a′ |
（3）已知存在单位向量
| b |
| a |
| a′ |
| b |
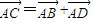，则ABCD为平行四边形
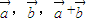为非零向量，且a+b平分a与b的夹角，则|a|=|b|