摘要:109.证明直线与直线的平行的思考途径 (1)转化为判定共面二直线无交点, (2)转化为二直线同与第三条直线平行, (3)转化为线面平行, (4)转化为线面垂直, (5)转化为面面平行.
网址:http://m.1010jiajiao.com/timu_id_4362175[举报]
 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.(Ⅰ)证明:中截面DEFG是梯形;
(Ⅱ)在△ABC中,记BC=a,BC边上的高为h,面积为S.在估测三角形ABC区域内正下方的矿藏储量(即多面体A1B1C1-A2B2C2的体积V)时,可用近似公式V估=S中-h来估算.已知V=
| 1 | 3 |
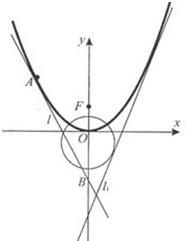 如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.
如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.(1)求m与a的值;
(2)设A是C1上的一动点,以A为切点作抛物线C1的切线l,直线l交y轴于点B,以FA,FB为邻边作平行四边形FAMB,证明:点M在一条定直线上;
(3)在(2)的条件下,记点M所在的定直线为l2,直线l2与y轴交点为N,连接MF交抛物线C1于P,Q两点,求△NPQ的面积S的取值范围. 查看习题详情和答案>>
已知曲线C:f(x)=x2,C上的点A0,An的横坐标分别为1和an(n∈N*),且a1=5,数列{xn}满足xn+1=t•f(xn-1)+1(t>0且t≠
,t≠1),设区间Dn=[1,an](an>1),当x∈Dn时,曲线C上存在点Pn(xn,f(xn)),使得点Pn处的切线与直线A0An平行.
(1)证明:{logt(xn-1)+1}是等比数列;
(2)当Dn+1?Dn对一切n∈N*恒成立时,求t的取值范围;
(3)记数列{an}的前n项和为Sn,当t=
时,试比较Sn与n+7的大小,并证明你的结论.
查看习题详情和答案>>
| 1 |
| 2 |
(1)证明:{logt(xn-1)+1}是等比数列;
(2)当Dn+1?Dn对一切n∈N*恒成立时,求t的取值范围;
(3)记数列{an}的前n项和为Sn,当t=
| 1 |
| 4 |
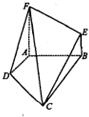 如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD. 已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点
已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点