摘要:2.计算并完成以下表格 n -3 -2 -1 0 1 2 3 教学环节与问题设计 设计目的 第一环节:创设游戏情境.设疑激趣 学生分成小组.动手折纸 , 观察对折次数与所得纸的层数的关系.得出折一次为 2 层纸.折两次为 22层纸 , 折三次为 23 层纸 ...得对折次数x与所得纸的层数 y 的关系式为 y =2x 设疑激趣.在学生动手操作的过程中激发学生学习热情和探索新知的欲望. 第二环节:引出具体定义.探究条件 定义: 一般地 , 函数 = (且) 叫做指数函数 , 其中 是自变量 , 定义域为 R. 问题:为何对有这样的要求? (1) 如果=0 当 >0 时 恒等于 0; 当 〈 0 时 , 无意义 (2) 如果〈 0 时,比如: .对及等都无意义 (3) 如果 =1, 则原函数变成是一个常数 , 研究价值不大. 对a的范围的具体分析.有利于学生对指数函数一般形式的掌握.同时为后面研究函数的图象和性质埋下了伏笔. 第三环节:运用定义.判断具体函数 能否判断下列函数哪些是指数函数吗? (1) (2) (3) (4) 打破学生对定义的轻视并使学生头脑中不断完善对定义理解
网址:http://m.1010jiajiao.com/timu_id_4357627[举报]
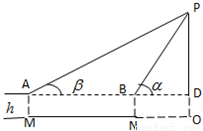
(2012•荆州模拟)OP是底部O不能到达的高塔,P是高塔的最高点,选择一条水平基线M,N,使得M,N,O三点在同一条直线上,在相距为d的M,N两点用测角仪测得P的仰角分别为α,β,已知测角仪高h=1.5m,试完成如下《实验报告》

(要求:(1)计算两次测量值的平均值并填入表格;(2)利用α,β,d的平均值,求OP的值,写出详细的计算过程;
(3)把计算结果填入表格.(相关数据:)
查看习题详情和答案>>

(要求:(1)计算两次测量值的平均值并填入表格;(2)利用α,β,d的平均值,求OP的值,写出详细的计算过程;
(3)把计算结果填入表格.(相关数据:)
| 题目 | 测量底部不能到达的高塔的高度 | 计算过程 | |||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 | |
| α | 75°32′ | 74°28′ | |||
| β | 30°17′ | 29°43′ | |||
| d(m) | 59.82 | 60.18 | |||
| 测量目标 | |||||
| 结果 | |||||
三角函数内容丰富,公式很多.如果你仔细观察、敢于设想、科学求证,那么你也能发现其中的一些奥秘.请你完成以下问题:
(1)计算:(直接写答案)
+
=
+
=
(2)根据(1)的计算结果,请你猜出一个一般性的结论:
+
=
+
=
.(用数学式子加以表达,并证明你的结论,写出推理过程.)
查看习题详情和答案>>
(1)计算:(直接写答案)
| cos2° |
| sin47° |
| cos88° |
| sin133° |
| 2 |
| 2 |
| cos5° |
| sin50° |
| cos85° |
| sin130° |
| 2 |
| 2 |
(2)根据(1)的计算结果,请你猜出一个一般性的结论:
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
| cos(θ-45°) |
| sinθ |
| cos(135°-θ) |
| sin(180°-θ) |
| 2 |
OP是底部O不能到达的高塔,P是高塔的最高点,选择一条水平基线M,N,使得M,N,O三点在同一条直线上,在相距为d的M,N两点用测角仪测得P的仰角分别为α,β,已知测角仪高h=1.5m,试完成如下《实验报告》
(要求:(1)计算两次测量值的平均值并填入表格;(2)利用α,β,d的平均值,求OP的值,写出详细的计算过程;
(3)把计算结果填入表格.(相关数据:)
查看习题详情和答案>>

(要求:(1)计算两次测量值的平均值并填入表格;(2)利用α,β,d的平均值,求OP的值,写出详细的计算过程;
(3)把计算结果填入表格.(相关数据:)
| 题目 | 测量底部不能到达的高塔的高度 | 计算过程 | |||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 | |
| α | 75°32′ | 74°28′ | |||
| β | 30°17′ | 29°43′ | |||
| d(m) | 59.82 | 60.18 | |||
| 测量目标 | |||||
| 结果 | |||||
查看习题详情和答案>>
探究函数f(x)=2x+
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数f(x)=2x+
(x>0)在区间(0,2)上递减;函数f(x)=2x+
(x>0)在区间
(2)证明:函数f(x)=2x+
(x>0)在区间(0,2)递减.
(3)思考:函数f(x)=2x+
(x<0)时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
查看习题详情和答案>>
| 8 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数f(x)=2x+
| 8 |
| x |
| 8 |
| x |
(2,+∞)
(2,+∞)
上递增.当x=2
2
时,y最小=4
4
.(2)证明:函数f(x)=2x+
| 8 |
| x |
(3)思考:函数f(x)=2x+
| 8 |
| x |
探究函数f(x)=x+
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
请观察表中值y随x值变化的特点,完成以下的问题.
函数f(x)=x+
(x>0)在区间(0,2)上递减;
函数f(x)=x+
(x>0)在区间
当x=
证明:函数f(x)=x+
(x>0)在区间(0,2)递减.
思考:(直接回答结果,不需证明)
(1)函数f(x)=x+
(x<0)有没有最值?如果有,请说明是最大值还是最小值,以及取相应最值时x的值.
(2)函数f(x)=ax+
,(a<0,b<0)在区间
查看习题详情和答案>>
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
| 4 |
| x |
函数f(x)=x+
| 4 |
| x |
(2,0)
(2,0)
上递增.当x=
2
2
时,y最小=4
4
.证明:函数f(x)=x+
| 4 |
| x |
思考:(直接回答结果,不需证明)
(1)函数f(x)=x+
| 4 |
| x |
(2)函数f(x)=ax+
| b |
| x |
[-
,0)
|
[-
,0)
和
|
(0,
]
|
(0,
]
上单调递增.
|