摘要: 函数的周期性. (1)类比“三角函数图像 得: ①若图像有两条对称轴.则必是周期函数.且一周期为, ②若图像有两个对称中心.则是周期函数.且一周期为, ③如果函数的图像有一个对称中心和一条对称轴.则函数必是周期函数.且一周期为, 如已知定义在上的函数是以2为周期的奇函数.则方程在上至少有 个实数根 (2)由周期函数的定义“函数满足.则是周期为的周期函数 得: ①函数满足.则是周期为2的周期函数, ②若恒成立.则, ③若恒成立.则. 如(1) 设是上的奇函数..当时..则等于 (答:),(2)定义在上的偶函数满足.且在上是减函数.若是锐角三角形的两个内角.则的大小关系为 (答:),(3)已知是偶函数.且=993.=是奇函数.求的值设是定义域为R的函数.且.又.则= (答:)
网址:http://m.1010jiajiao.com/timu_id_4357261[举报]
由已知得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以函数f(x)的值以6为周期重复性出现.,所以f(2009)= f(5)=1,故选C.
答案:C.
【命题立意】:本题考查归纳推理以及函数的周期性和对数的运算.
查看习题详情和答案>>
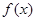 的定义域为
的定义域为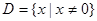 ,且满足对于任意
,且满足对于任意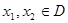 ,有
,有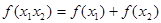 .
.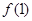 的值;
的值;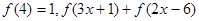 ≤
≤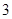 ,且
,且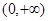 上是增函数,求
上是增函数,求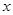 的取值范围.
的取值范围.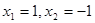 ,求出f(1)0;
,求出f(1)0;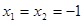 ,得
,得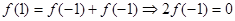 .令
.令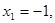
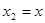 ,得
,得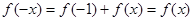 ,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.