在圆锥曲线与直线联立求解时.消元后得到的方程.要注意其二次项系数是否为零?△≥0的限制.(求交点.弦长.中点.斜率.对称存在性问题都在△≥0下进行.)——青夏教育精英家教网——

摘要：在圆锥曲线与直线联立求解时.消元后得到的方程.要注意其二次项系数是否为零?△≥0的限制.(求交点.弦长.中点.斜率.对称存在性问题都在△≥0下进行.)

网址：http://m.1010jiajiao.com/timu_id_4356828[举报]

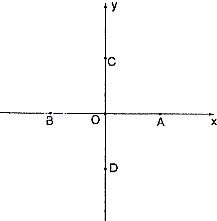在直角坐标系XOY中，已知点A（1，0），B（-1，0），C（0，1），D（0，-1），动点M满足

|），其中m是参数（m∈R）
（I）求动点M的轨迹方程，并根据m的取值讨论方程所表示的曲线类型；
（II）当动点M的轨迹表示椭圆或双曲线，且曲线与直线l：y=x+2交于不同的两点时，求该曲线的离心率的取值范围．查看习题详情和答案>>

我们把正切函数在整个定义域内的图象看作一组“平行曲线”，而“平行曲线”具有性质：任意两条平行直线与两条相邻的“平行曲线”相交，被截得的线段长度相等．已知函数f(x)=tan(ωx+

)(ω＞0)图象中的两条相邻“平行曲线”与直线y=2013相交于A，B两点，且|AB|=2，f（2）=（　　）

查看习题详情和答案>>

动点P在x轴与直线l：y=3之间的区域（含边界）上运动，且到点F（0，1）和直线l的距离之和为4．
（1）求点P的轨迹C的方程；
（2）过点Q（0，-1）作曲线C的切线，求所作的切线与曲线C所围成区域的面积．查看习题详情和答案>>

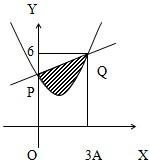已知曲线y=x²-2x+3与直线y=x+3相交于点P（0，3）、Q（3，6）两点．
（1）分别求出曲线在交点的切线的斜率；
（2）求出曲线与直线所围成的图形的面积．查看习题详情和答案>>

(本题分12分）

定义.

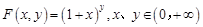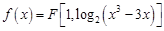（Ⅰ）求曲线与直线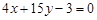垂直的切线方程；

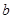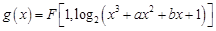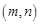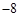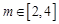（Ⅱ）若存在实数使曲线在点处的切线斜率为,且,求实数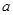的取值范围.

查看习题详情和答案>>