Question

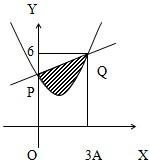已知曲线y=x²-2x+3与直线y=x+3相交于点P（0，3）、Q（3，6）两点．
（1）分别求出曲线在交点的切线的斜率；
（2）求出曲线与直线所围成的图形的面积．

Answer 1

分析：（1）函数y=f（x）在某点的导数值即为在该点的斜率，所以只要求出该点的导数值即可．
（2）求图形的面积，根据图形只要求出梯形OAQP的面积与曲边梯形OAQP的面积，求曲边梯形OAQP的面积，用定积分求，再求它们之差即可．

解答：解：（1）∵y=x²-2x+3，
∴y′=2x-2，
∴过点（0，3）的切线斜率
k₁=y′|_x=0=-2．
过点（3，6）的切线斜率
k₁=y′|_x=3=4．

（2）设所求的带阴影的图形的面积为S，则S为梯形OAQP的面积与曲边梯形OAQP的面积的差．
而梯形OAQP的面积=

1

2

(OP+AQ)•OA=

27

2

．
曲边梯形OAQP的面积=

∫

3 0

(x2-2x+3)dx=(

1

3

x3-x2+3x)|_3=9
∴S=

27

2

-9=4.5．

答：（1）过点（0，3）的切线斜率为-2．过点（3，6）的切线斜率为4．
（2）曲线与直线所围成的图形的面积为4.5．

点评：函数y=f（x）在某点的导数值即为在该点的斜率，过（x．y．）点的切线方程为：y-y．=y'|_x=x．（x-x．）；
求曲边梯形的面积，常用定积分求．