摘要: 判断直线与圆锥曲线的位置关系时.通常将直线的方程代入圆锥曲线的方程.消去(也可以消去)得到一个关于变量(或者变量)的一元二次方程. 即.消去后的. (1)当时.则有.直线与曲线相交,.直线与曲线相切,.直线与曲线相离. (2)当时.即得到一个一次方程.则与相交.且只有一个交点.此时.若为双曲线.则直线与双曲线的渐近线是平行,若为抛物线.则直线与抛物线的对称轴的位置关系是平行.
网址:http://m.1010jiajiao.com/timu_id_4355957[举报]
(2012•湖北)设A是单位圆x2+y2=1上的任意一点,i是过点A与x轴垂直的直线,D是直线i与x轴的交点,点M在直线l上,且满足丨DM丨=m丨DA丨(m>0,且m≠1).当点A在圆上运动时,记点M的轨迹为曲线C.
(I)求曲线C的方程,判断曲线C为何种圆锥曲线,并求焦点坐标;
(Ⅱ)过原点且斜率为k的直线交曲线C于P、Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.
查看习题详情和答案>>
(I)求曲线C的方程,判断曲线C为何种圆锥曲线,并求焦点坐标;
(Ⅱ)过原点且斜率为k的直线交曲线C于P、Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.
已知△ABC的两个顶点A,B的坐标分别是(0,-1),(0,1),且AC,BC所在直线的斜率之积等于m(m≠0).
(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-
时,过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M,Q不重合) 试问:直线MQ与x轴的交点是否为定点?若是,求出定点,若不是,请说明理由.
查看习题详情和答案>>
(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-
| 1 | 2 |
(本大题满分14分)
已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,
, ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于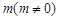 .
.
(Ⅰ)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点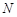 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合).求证直线
不重合).求证直线 与
与 轴的交点为定点,并求出该定点的坐标.
轴的交点为定点,并求出该定点的坐标.
查看习题详情和答案>>
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.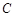 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.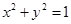 上任意一点,
上任意一点, 是过点
是过点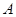 与
与 轴垂直的直线,
轴垂直的直线,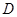 是直线
是直线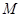 在直线
在直线 ,当点
,当点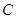 。
。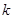 的直线交曲线
的直线交曲线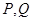 两点,其中
两点,其中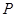 在第一象限,且它在
在第一象限,且它在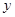 轴上的射影为点
轴上的射影为点 ,直线
,直线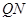 交曲线
交曲线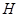 ,是否存在
,是否存在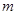 ,使得对任意的
,使得对任意的 ,都有
,都有 ?若存在,请说明理由。
?若存在,请说明理由。