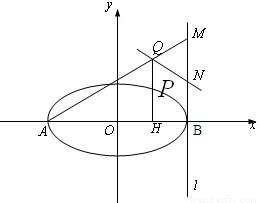
摘要：例1 如图.已知是圆的直径.垂直于所在的平面.是圆周上不同于的任一点.求证:平面平面． 分析:根据“面面垂直 的判定定理.要证明两平面互相垂直.只要在其中一个平面中寻找一条与另一平面垂直的直线即可 解:∵是圆的直径.∴. 又∵垂直于所在的平面.∴. ∴平面.又在平面中. 所以.平面平面． 说明:由于平面与平面相交于.所以如果平面平面.则在平面中.垂直于的直线一定垂直于平面.这是寻找两个平面的垂线的常用方法 例2．已知.求证:． 证明:设. 在内取点.过作于.于点. ∵.∴. 又∵. ∴.同理可得. ∴． 例3．已知在一个的二面角的棱长有两点.分别是在这个二面角的两个平面内.且垂直于线段.又知.求的长 解:由已知 . ∴ .
网址：http://m.1010jiajiao.com/timu_id_4354265[举报]
如图，已知椭圆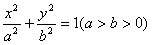
的长轴为AB，过点B的直线l与x轴垂直，直线（2-k）x-（1+2k）y+（1+2k）=0（k∈R）所经过的定点恰好是椭圆的一个顶点，且椭圆的离心率
，
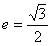（1）求椭圆的标准方程；
（2）设P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP=PQ，连接AQ并延长交直线l于点M，N为MB的中点，试判断直线QN与以AB为直径的圆O的位置关系。
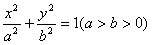的长轴为AB，过点B的直线l与x轴垂直，直线（2-k）x-（1+2k）y+（1+2k）=0（k∈R）所经过的定点恰好是椭圆的一个顶点，且椭圆的离心率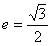，（1）求椭圆的标准方程；
（2）设P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP=PQ，连接AQ并延长交直线l于点M，N为MB的中点，试判断直线QN与以AB为直径的圆O的位置关系。
如图， 已知椭圆
的长轴为
，过点
的直线
与
轴垂直．直线
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
.
（1）求椭圆的标准方程；
（2）设
是椭圆上异于
、的任意一点，
轴，
为垂足，延长
到点
使得
，连结
延长交直线于点
，
为
的中点．试判断直线
与以为直径的圆
的位置关系．
如图， 已知椭圆
的长轴为
，过点
的直线
与
轴垂直．直线
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
.
（1）求椭圆的标准方程；
（2）设
是椭圆上异于
、的任意一点，
轴，
为垂足，延长
到点
使得
，连结
延长交直线于点
，
为
的中点．试判断直线
与以为直径的圆
的位置关系．
的长轴为
，过点
的直线
与
轴垂直．直线
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
.
是椭圆上异于
、
轴，
为垂足，延长
到点
使得
，连结
延长交直线
，
为
的中点．试判断直线
与以
的位置关系．
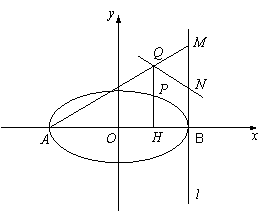
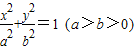的长轴为AB，过点B的直线l与x轴垂直．直线（2-k）x-（1+2k）y+（1+2k）=0（k∈R）所经过的定点恰好是椭圆的一个顶点，且椭圆的离心率
．