摘要:=sin(2x+)(-<<0).y=f(x)图象的一条对称轴是直线x=. (1)求, 的单调增区间, (3)证明:直线5x-2y+c=0与函数y=f(x)的图象不相切. (1)解 ∵x=是函数y=f(x)的图象的对称轴. ∴sin =±1. ∴+=k+.k∈Z. ∵-<<0.∴=-. 知=-.因此y=sin. 由题意得2k-≤2x-≤2k+.k∈Z. 则k+≤x≤k+.k∈Z 所以函数y=sin的单调增区间为 .k∈Z. (3)证明 ∵|y′|=|(sin())′| =|2cos()|≤2. ∴曲线y=f(x)的切线斜率的取值范围是[-2.2].而直线5x-2y+c=0的斜率为>2.所以直线5x-2y+c=0与函数 y=sin()的图象不相切.
网址:http://m.1010jiajiao.com/timu_id_4353270[举报]
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一个对称中心的坐标为(- ,0).
,0).
(1)求φ;
(2)作出函数y=f(x)在区间[0,π]上的图象;

(3)试求x∈R时函数f(x)的最小值,并求相应的x的取值集合
查看习题详情和答案>>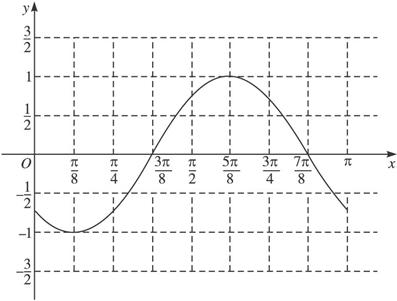
 .
.
 .
.