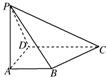
摘要:11.已知四棱锥P-ABCD的底面为直角梯形.AB∥DC.底面ABCD.且PA=AD=DC=AB=1.M是PB的中点. (1)求AC与PB所成的角, (2)求面AMC与面BMC所成二面角的大小. 解:(1)过点B作BE//CA.且BE=CA.则 ∠PBE是AC与PB所成的角. 连结AE.可知AC=CB=BE=AE=.又AB=2.所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°,在Rt△PEB中BE=.PB=. (2)作AN⊥CM.垂足为N.连结BN.在Rt△PAB中.AM=MB. 又AC=CB.∴△AMC≌△BMC,∴BN⊥CM. 故∠ANB为所求二面角的平面角. ∵CB⊥AC.由三垂线定理.得CB⊥PC.在Rt△PCB中.CM=MB.所以CM=AM. 在等腰三角形AMC中.AN·MC=. . ∴AB=2,, 故所求的二面角为
网址:http://m.1010jiajiao.com/timu_id_4353127[举报]
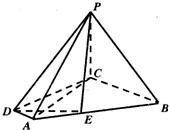 已知四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=
已知四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=| π | 2 |
(I)求证:DE⊥平面PAC;
(II)求二面角B-PA-C的大小. 查看习题详情和答案>>
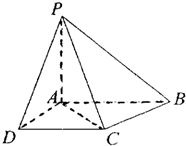 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 | 2 |
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成角的余弦值. 查看习题详情和答案>>
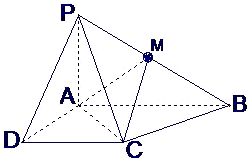 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 | 2 |
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小. 查看习题详情和答案>>
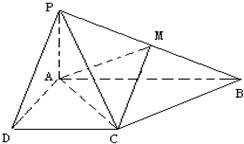 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.