摘要:12.已知f(x)是实数集R上的函数.且对任意x∈R.f(x)=f(x+1)+f(x-1)恒成立. (1)求证:f(x)是周期函数, (2)已知f(3)=2.求f. (1)证明:∵f(x)=f(x+1)+f(x-1) ∴f(x+1)=f(x)-f(x-1). 则f(x+2)=f[(x+1)+1]=f(x+1)-f(x) =f(x)-f(x-1)-f(x)=-f(x-1). ∴f(x+3)=f[(x+1)+2]=-f[(x+1)-1]=-f(x). ∴f(x+6)=f[(x+3)+3]=-f(x+3)=f(x). ∴f(x)是周期函数且6是它的一个周期. (2)解:f=f=f(0)=-f(3)=-2.
网址:http://m.1010jiajiao.com/timu_id_4347354[举报]
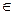 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.