摘要：要理解并掌握二倍角公式以及推导.能正确运用二倍角的正弦.余弦.正切公式进行简单三角函数式的化简.求值与恒等式证明 二倍角公式是由和角公式由一般化归为特殊而来的.要注重这种基本数学思想方法.学会怎样去发现数学规律
网址：http://m.1010jiajiao.com/timu_id_4346826[举报]
已知tan110°=a，求tan50°时，同学甲利用两角差的正切公式求得：tan50°=
；同学乙利用二倍角公式及诱导公式得tan50°=
；根据上述信息可估算a是介于 两个连续整数之间．
查看习题详情和答案>>
a-
| ||
1+
|
| 1-a2 |
| 2a |
类比“二倍角的正、余弦公式”的形式，对于给定的两个函数，f(x)=
，g(x)=
，给出以下两个式子
①f（2x）=2f（x）•g（x）； ②g（2x）=[g（x）]2-[f（x）]2；
其中正确的是
查看习题详情和答案>>
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
①f（2x）=2f（x）•g（x）； ②g（2x）=[g（x）]2-[f（x）]2；
其中正确的是
①
①
．已知tan110°=a，求tan50°时，同学甲利用两角差的正切公式求得：tan50°=
；同学乙利用二倍角公式及诱导公式得tan50°=
；根据上述信息可估算a的范围是（ ）
a-
| ||
1+
|
| 1-a2 |
| 2a |
A、-∞，-2-
| ||
B、-2-
| ||
| C、（-3，-2） | ||
D、(-2，-
|
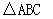中，内角A，B，C所对的分别是a,b，c。已知a=2，c=
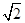,cosA=
.
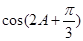的值。
的图象向左平移
个单位,得到函数
即
的图象,再向上平移1个单位,所得图象的函数解析式为
,故选B.