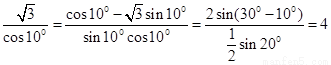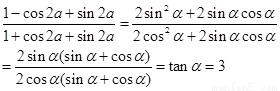题目内容
类比“二倍角的正、余弦公式”的形式,对于给定的两个函数,f(x)=
,g(x)=
,给出以下两个式子
①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
其中正确的是
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
其中正确的是
①
①
.分析:写出“二倍角的正弦公式”的形式,据此二倍角公式写出类比结论,最后再进行证明即可.
解答:解:∵“二倍角的正弦公式”的形式是:
sin2x=2sinxcosx,cos2x=cos2x-sin2x,
有类比结论:
设f(x)=
,g(x)=
,有①f(2x)=2f(x)•g(x); ②g(2x)=[g(x)]2-[f(x)]2;
其中①是正确的,证明如下:
∵f(x)=
,g(x)=
,
∴f(x)g(x)=
×
=
×
=
f(2x)
∴f(2x)=2f(x)g(x).
②是不正确的,∵证明如下:
由于g(2x)=
,
[g(x)]2-[f(x)]2=(
)2-(
)2=1,
故②不正确.
故答案为:①.
sin2x=2sinxcosx,cos2x=cos2x-sin2x,
有类比结论:
设f(x)=
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
其中①是正确的,证明如下:
∵f(x)=
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
∴f(x)g(x)=
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
| 1 |
| 2 |
| e2x-e-2x |
| 2 |
| 1 |
| 2 |
∴f(2x)=2f(x)g(x).
②是不正确的,∵证明如下:
由于g(2x)=
| e2x+e-2x |
| 2 |
[g(x)]2-[f(x)]2=(
| ex+e-x |
| 2 |
| ex-e-x |
| 2 |
故②不正确.
故答案为:①.
点评:本题考查利用类比推理从形式上写出类比结论,写类比结论时:先找类比对象,再找类比元素.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
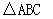 中,内角A,B,C所对的分别是a,b,c。已知a=2,c=
中,内角A,B,C所对的分别是a,b,c。已知a=2,c=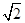 ,cosA=
,cosA= .
.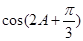 的值。
的值。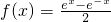 ,
,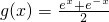 ,给出以下两个式子
,给出以下两个式子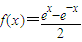 ,
,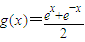 ,给出以下两个式子
,给出以下两个式子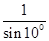 -
-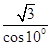 的值;
的值;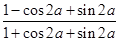 的值.
的值.