摘要:4.观察下面两个图的阴影部分.它们同集合A.集合B有什么关系? 如上图.集合A和B的公共部分叫做集合A和集合B的交.集合A和B合并在一起得到的集合叫做集合A和集合B的并. 观察问题3中A.B.C三个集合的元素关系易知.集合C={1.2}是由所有属于集合A且属于集合B的元素所组成的.即集合C的元素是集合A.B的公共元素.此时.我们就把集合C叫做集合A与B的交集.这是今天我们要学习的一个重要概念. 问题:观察下列两组集合.说出集合A与集合B的关系 (1)A={1.2.3}.B={1.2.3.4.5} (2)A=N.B=Q (3)A={-2.4}. (集合A中的任何一个元素都是集合B的元素)
网址:http://m.1010jiajiao.com/timu_id_4346777[举报]
观察下面两个推理过程及结论:
若锐角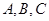 满足
满足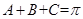 ,以角
,以角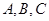 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: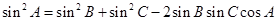 ,
,
若锐角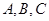 满足
满足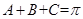 ,则
,则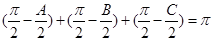 ,以角
,以角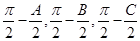 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: .
.
则:若锐角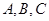 满足
满足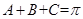 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
查看习题详情和答案>>
观察下面两个推理过程及结论:
(1) 若锐角A, B, C满足A+B+C=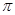 , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: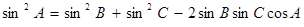
(2) 若锐角A, B, C满足A+B+C=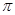 , 则
, 则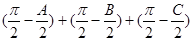 =
=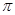 , 以
, 以
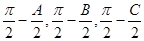 分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
得到的等式: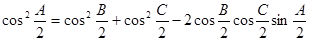 则:若锐角A, B, C满
则:若锐角A, B, C满
足A+B+C=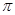 , 类比上面推理方法, 可以得到一个等式是 .
, 类比上面推理方法, 可以得到一个等式是 .
查看习题详情和答案>>
观察下面两个推理过程及结论:
若锐角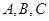 满足
满足 ,以角
,以角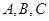 分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式: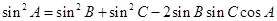 ,
,
若锐角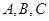 满足
满足 ,则
,则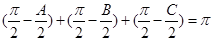 ,以角
,以角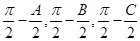 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式:
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式: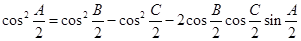 .
.
则:若锐角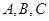 满足
满足 ,类比上面推理方法,可以得到的一个等式是______________.
,类比上面推理方法,可以得到的一个等式是______________.
查看习题详情和答案>>