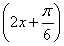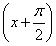摘要:已知a>0.函数f(x)=-2asin+2a+b,当x∈时.-5≤f(x)≤1. (1)求常数a,b的值, =f且lg g的单调区间. 解 (1)∵x∈.∴2x+∈. ∴sin∈. ∴-2asin∈[-2a,a]. ∴f(x)∈[b,3a+b], 又∵-5≤f(x)≤1,因此可得b=-5,3a+b=1, 因此a=2,b=-5. 知a=2,b=-5, ∴f(x)=-4sin-1, g(x)=f=-4sin-1 =4sin-1. 又由lg g>1,∴4sin-1>1, ∴sin>, ∴2k+<2x+<2k+,k∈Z. 由2k+<2x+≤2k+的单调增区间为: 由2k+≤2x+<2k+, 得g(x)的单调减区间为.
网址:http://m.1010jiajiao.com/timu_id_4346240[举报]
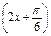 +2a+b,当x∈
+2a+b,当x∈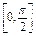 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.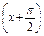 且lg g(x)>0,求g(x)的单调区间.
且lg g(x)>0,求g(x)的单调区间. +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1. 且lgg(x)>0,求g(x)的单调区间.
且lgg(x)>0,求g(x)的单调区间.