摘要：设a=,b==a·b. 的解析式, (2)已知常数＞0.若y=f(x)在区间上是增函数.求的取值范围, (3)设集合A=.B={x||f(x)-m|＜2},若AB.求实数m的取值范围. 解 =sin2·4sinx+· =4sinx·+cos2x =2sinx+1-2sin2x=2sinx+1, ∴f(x)=2sinx+1. (2)∵f(x)=2sinx+1,＞0. 由2k-≤x≤2k+, 得f(x)的增区间是,k∈Z. ∵f(x)在上是增函数. ∴. ∴-≥且≤,∴∈. -m|＜2,得-2＜f(x)-m＜2, 即f+2. ∵AB.∴当≤x≤时. 不等式f+2恒成立. ∴f(x)max-2＜m＜f(x)min+2, ∵f(x)max=f()=3,f(x)min=f()=2,∴m∈(1.4).
网址：http://m.1010jiajiao.com/timu_id_4346238[举报]
设a＝
，b＝(4sinx，cosx－sinx)，f(x)＝a·b.
(1)求函数f(x)的解析式；
(2)已知常数ω＞0，若y＝f(ωx)在区间
上是增函数，求ω的取值范围；
(3)设集合A＝
，B＝{x||f(x)－m|＜2}，若A
B，求实数m的取值范围．
设a＝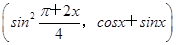
，b＝(4sinx，cosx－sinx)，f(x)＝a·b.
(1)求函数f(x)的解析式；
(2)已知常数ω＞0，若y＝f(ωx)在区间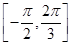
上是增函数，求ω的取值范围；
(3)设集合A＝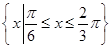
，B＝{x||f(x)－m|＜2}，若A
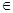B，求实数m的取值范围．
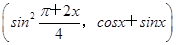，b＝(4sinx，cosx－sinx)，f(x)＝a·b.(1)求函数f(x)的解析式；
(2)已知常数ω＞0，若y＝f(ωx)在区间
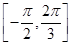上是增函数，求ω的取值范围；(3)设集合A＝
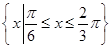，B＝{x||f(x)－m|＜2}，若AB，求实数m的取值范围．设a＝
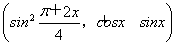，b＝(4sinx，cosx－sinx)，f(x)＝a·b.
(1)求函数f(x)的解析式；
(2)已知常数ω＞0，若y＝f(ωx)在区间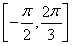
上是增函数，求ω的取值范围；
(3)设集合A＝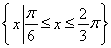
，B＝{x||f(x)－m|＜2}，若A
B，求实数m的取值范围．
查看习题详情和答案>>
,b=(4sinx,cosx-sinx),f(x)=a·b.
＞0，若y=f(
上是增函数，求
，B={x||f(x)-m|＜2},若A
B，求实数m的取值范围.