摘要: 一个多面体的三视图和直观图如图所示.其中D为A A1的中点. (1)求平面B1DC把多面体ABC-A1B1C1分成两部分的体积之比. (2)在线段B1C上是否存在一点E.使A1E//平面BDC,若存在指出E点的位置.若不存在.说明理由. (3)求直线BD与平面B1DC夹角的正弦值. 19 解:(1)由三视图可知直观图为直三棱柱且底面ABC中.BC⊥AC.BC=CC1=2.AC=1. . 所以两部分体积之比为1:1 4分 (2)取B1C的中点E.BC中点F.连EF,A1E,DF.易证A1DFE为平行四边形.所以A1E∥DF.而DF面BDC.A1E面BDC.所以A1E∥面BDC 即存在E点.当E为B1C中点时有A1E∥面BDC 8分 (3)连C1D.易知CD⊥C1D.又CD⊥B1C1.所以CD⊥面B1C1D 所以面B1DC⊥面B1C1D.作C1M⊥B1D.则C1M⊥面B1DC 可求C1M=.即B点到面B1DC的距离为.又BD= 所以BD与面B1DC夹角的正弦值= 12分
网址:http://m.1010jiajiao.com/timu_id_4344406[举报]
(本小题满分12分)
下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.

(1)请在正视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程);
(2)求该多面体的体积(尺寸如图).
查看习题详情和答案>>
(本小题满分12分)一个多面体的直观图和三视图如图所示,其中 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证: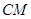
 平面
平面
(2)在线段 上(含
上(含 、
、 端点)确定一点
端点)确定一点 ,使得
,使得
 平面
平面 ,并给出证明;
,并给出证明;
(3)一只小飞虫在几何体 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体 内的概率.
内的概率.


查看习题详情和答案>>

 的值;若不存在,说明理由.
的值;若不存在,说明理由. (1)求证:
(1)求证: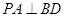 ;(2)是否在线段
;(2)是否在线段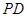 上存在一
上存在一 点,使二面角
点,使二面角 的平
的平 ,设
,设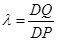 ,若存在,求
,若存在,求 ;若不存在,说明理由
;若不存在,说明理由
