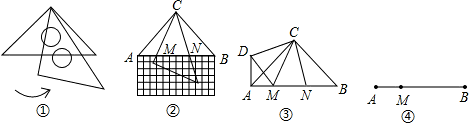
摘要: 解:(1)将图1中的正方形等分成如图的四个小正方形.将这4个转发装置安装在这4个小正方形对角线的交点处.此时.每个小正方形的对角线长为.每个转发装置都能完全覆盖一个小正方形区域.故安装4个这种装置可以达到预设的要求. ····················· (2)将原正方形分割成如图2中的3个矩形.使得.将每个装置安装在这些矩形的对角线交点处.设.则.. 由.得. .. 即如此安装3个这种转发装置.也能达到预设要求.·············································· 或:将原正方形分割成如图2中的3个矩形.使得.是的中点.将每个装置安装在这些矩形的对角线交点处.则.. .即如此安装三个这个转发装置.能达到预设要求.···················································································· 要用两个圆覆盖一个正方形.则一个圆至少要经过正方形相邻两个顶点.如图3.用一个直径为31的去覆盖边长为30的正方形.设经过.与交于.连.则.这说明用两个直径都为31的圆不能完全覆盖正方形. 所以.至少要安装3个这种转发装置.才能达到预设要求.··································· 评分说明:示意图每个图1分. 30解:(1),.. (2)设存在实数.使抛物线上有一点.满足以为顶点的三角形与等腰直角相似. 以为顶点的三角形为等腰直角三角形.且这样的三角形最多只有两类.一类是以为直角边的等腰直角三角形.另一类是以为斜边的等腰直角三角形. ①若为等腰直角三角形的直角边.则. 由抛物线得:.. ..的坐标为. 把代入抛物线解析式.得. 抛物线解析式为. 即. ②若为等腰直角三角形的斜边. 则.. 的坐标为. 把代入抛物线解析式.得. 抛物线解析式为.即 当时.在抛物线上存在一点满足条件.如果此抛物线上还有满足条件的点.不妨设为点.那么只有可能是以为斜边的等腰直角三角形.由此得.显然不在抛物线上.因此抛物线上没有符合条件的其他的点. 当时.同理可得抛物线上没有符合条件的其他的点. 当的坐标为.对应的抛物线解析式为时. 和都是等腰直角三角形.. 又.. ..总满足. 当的坐标为.对应的抛物线解析式为时. 同理可证得:.总满足
网址:http://m.1010jiajiao.com/timu_id_4332101[举报]
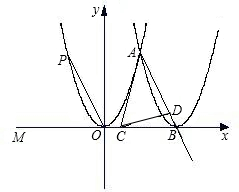
如图,点P(-m,m2)抛物线:y=x2上一点,将抛物线E沿x轴正方向平移2m个单位得到抛物线F,抛物线F的顶点为B,抛物线F交抛物线E于点A,点C是x轴上点B左侧一动点,点D是射线AB上一点,且∠ACD=∠POM.问△ACD能否为等腰三角形?若能,求点C的坐标;若不能,请说明理由.
说明:
(1)如果你反复探索,没有解决问题,请写出探索过程(要求至少写3步);
(2)在你完成(1)之后,可以从①、②中选取一个条件,完成解答(选取①得7分;选取②得10分).①m=1;②m=2. 查看习题详情和答案>>

说明:
(1)如果你反复探索,没有解决问题,请写出探索过程(要求至少写3步);
(2)在你完成(1)之后,可以从①、②中选取一个条件,完成解答(选取①得7分;选取②得10分).①m=1;②m=2. 查看习题详情和答案>>
28、如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形.
(1)图b中的阴影部分面积为
(2)观察图b,请你写出三个代数式(m+n)2,(m-n)2,mn之间的等量关系是
(3)若x+y=-6,xy=2.75,利用(2)提供的等量关系计算:x-y=
(4)实际上有许多代数恒等式可以用图形的面积来表示,如图C,它表示了
2m2+3mn+n2=(2m+n)(m+n),试画出一个几何图形的面积是a2+4ab+3b2,并能利用这个
图形将a2+4ab+3b2进行因式分解.
查看习题详情和答案>>
(1)图b中的阴影部分面积为
m2-2mn+n2或(m-n)2
;(2)观察图b,请你写出三个代数式(m+n)2,(m-n)2,mn之间的等量关系是
(m+n)2
=
(m-n)2
+4mn
;(3)若x+y=-6,xy=2.75,利用(2)提供的等量关系计算:x-y=
±5
;(4)实际上有许多代数恒等式可以用图形的面积来表示,如图C,它表示了
2m2+3mn+n2=(2m+n)(m+n),试画出一个几何图形的面积是a2+4ab+3b2,并能利用这个
图形将a2+4ab+3b2进行因式分解.

 如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在下面虚框中画出图形,并根据图形回答(2a+b)(a+2b)=
2a2+5ab+2b2
2a2+5ab+2b2
.(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.
①你画的图中需要C类卡片
6
6
张.
②可将多项式a2+5ab+6b2分解因式为
(a+2b)(a+3b)
(a+2b)(a+3b)
.
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式
ABCD
ABCD
(填写选项).A.xy=
| m2-n2 |
| 4 |
| m2+n2 |
| 2 |