Question

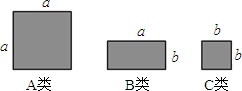
如图，有足够多的边长为a的小正方形（A类）、长为a宽为b的长方形（B类）以及边长为b的大正方形（C类），发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．
比如图②可以解释为：（a+2b）（a+b）=a²+3ab+2b²
（1）取图①中的若干个（三种图形都要取到）拼成一个长方形，使其面积为（2a+b）（a+2b），在下面虚框中画出图形，并根据图形回答（2a+b）（a+2b）=

2a²+5ab+2b²

．
（2）若取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为a²+5ab+6b²．
①你画的图中需要C类卡片

6

张．
②可将多项式a²+5ab+6b²分解因式为

（a+2b）（a+3b）

．

（3）如图③，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个矩形的两边长（x＞y），观察图案，指出以下正确的关系式

ABCD

（填写选项）．
A．xy=

m2-n2

4

，B．x+y=m，C．x²-y²=m•n，D．x²+y²=

m2+n2

2

．

Answer 1

分析：（1）画出图形，结合图象和面积公式得出即可；
（2）根据等式即可得出有6张，根据图形和面积公式得出即可；
（3）根据题意得出x+y=m，m²-n²=4xy，根据平方差公式和完全平方公式判断即可．

解答：解：（1）如图：

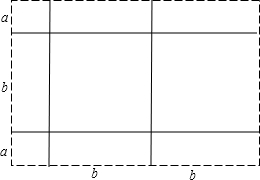
（2a+b）（a+2b）=2a²+5ab+2b²．
故答案为：2a²+5ab+2b²；

（2）①∵长方形的面积为a²+5ab+6b²，
∴画的图中需要C类卡片6张，
故答案为：6．

②a²+5ab+6b²=（a+2b）（a+3b），
故答案为：（a+2b）（a+3b）．

（3）解：根据图③得：x+y=m，
∵m²-n²=4xy，
∴xy=

m2-n2

4

，
x²-y²=（x+y）（x-y）=mn，
∴x²+y²=（x+y）²-2xy=m²-2×

m2-n2

4

=

m2+n2

2

，
∴选项A、B、C、D都正确．
故答案为：ABCD．

点评：本题考查了分解因式，长方形的面积，平方差公式，完全平方公式的应用，主要考查学生的观察图形的能力和化简能力．