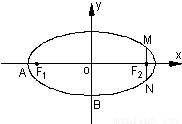
摘要:8. 如下图.设E:+=1(a>b>0)的焦点为F1与F2.且P∈E.∠F1PF2=2θ. 求证:△PF1F2的面积S=b2tanθ. 剖析:有些圆锥曲线问题用定义去解决比较方便.如本题.设|PF1|=r1.|PF2|=r2.则S=r1r2sin2θ.若能消去r1r2.问题即获解决. 证明:设|PF1|=r1.|PF2|=r2. 则S=r1r2sin2θ.又|F1F2|=2c. 由余弦定理有 (2c)2=r12+r22-2r1r2cos2θ=(r1+r2)2-2r1r2-2r1r2cos2θ=(2a)2-2r1r2(1+cos2θ). 于是2r1r2(1+cos2θ)=4a2-4c2=4b2. 所以r1r2=. 这样即有S=·sin2θ=b2=b2tanθ. 评述:解与△PF1F2(P为椭圆上的点)有关的问题.常用正弦定理或余弦定理.并结合|PF1|+|PF2|=2a来解决.
网址:http://m.1010jiajiao.com/timu_id_4067138[举报]
如下图,椭圆![]() =1(a>b>0)与过点A(2,0),B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0),B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=![]() ,
,

(1)求椭圆的方程;
(2)设F1、F2分别为椭圆的左、右焦点,求证:|AT|2=![]() |AF1||AF2|.
|AF1||AF2|.
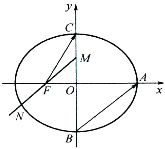 如图,在平面直角坐标系xOy中,已知点F是椭圆E:
如图,在平面直角坐标系xOy中,已知点F是椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| FC |
| BA |
| 1 |
| 2 |
(1)求椭圆E的方程;
(2)若P为线段FC(包括端点)上任意一点,当
| PA |
| PB |
(3)设M为线段BC(包括端点)上的一个动点,射线MF交椭圆于点N,若
| NF |
| FM |
如图,在直角坐标系xOy中,已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
直线与椭圆C相交M、N两点,且|MN|=1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左顶点为A,下顶点为B,动点P满足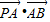 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
 查看习题详情和答案>>
查看习题详情和答案>>
 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的直线与椭圆C相交M、N两点,且|MN|=1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左顶点为A,下顶点为B,动点P满足
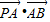 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上. 查看习题详情和答案>>
查看习题详情和答案>>
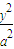 +
+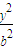 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=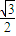 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的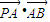 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.