摘要:3.性质:对于椭圆:(a>b>0)如下性质必须熟练掌握: ①范围; ②对称轴,对称中心; ③顶点; ④焦点; ⑤准线方程; ⑥离心率; 此外还有如下常用性质: ⑦焦半径公式: |PF1|==a+ex0.|PF2|==a-ex0, ⑧焦准距,准线间距;通径长; ⑨最大角 证:设|PF1|=r1,|PF2|=r2,则 对于椭圆:(a>b>0)的性质可类似的给出.
网址:http://m.1010jiajiao.com/timu_id_4067111[举报]
椭圆与双曲线有许多优美的对偶性质,如对于椭圆有如下命题:AB是椭圆
+
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
.那么对于双曲线则有如下命题:AB是双曲线
-
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
| x2 |
| a2 |
| y2 |
| b2 |
椭圆与双曲线有许多优美的对偶性质,如对于椭圆有如下命题:AB是椭圆 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
椭圆与双曲线有许多优美的对偶性质,如对于椭圆有如下命题:AB是椭圆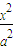 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
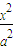 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
查看习题详情和答案>>
 +
+ =1(a>b>0)(离心率为黄金分割比
=1(a>b>0)(离心率为黄金分割比 的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线
的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线 -
- =1(a>b>0)(离心率为黄金分割比的倒数
=1(a>b>0)(离心率为黄金分割比的倒数 的双曲线)的左顶点、右焦点和其虚轴的上端点,则有( )
的双曲线)的左顶点、右焦点和其虚轴的上端点,则有( ) +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线